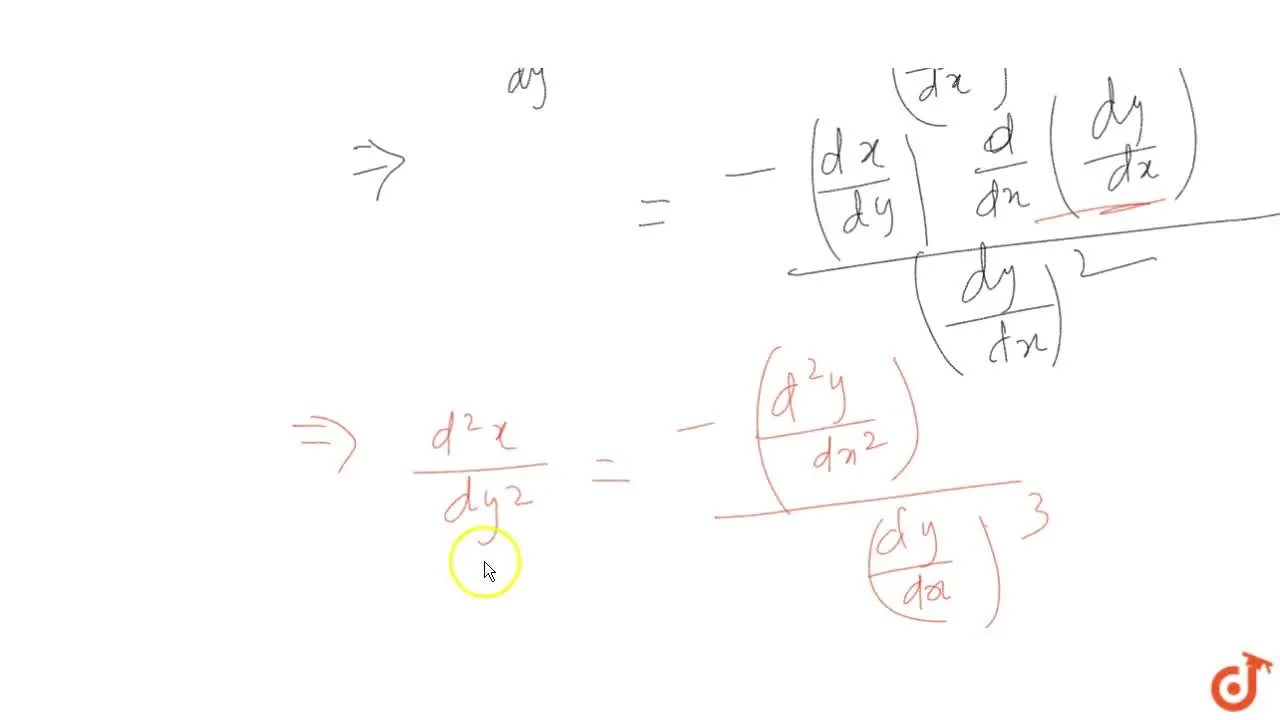
In is a independent variable and is the dependent variable. If independent and dependent variables are interchanged becomes and these two are connected by the relation . Find a relation between .
Video Solution
Text Solution
Given that,
so,
differentiate wrt we get,
which is the required relation between
.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
In dydx, x is independent variable and y is the dependent variable. If independent and dependent variables are interchanged dydx becomes dxdy and these two are connected by the relation dydx⋅dxdy=1 . Find a relation between d2ydx2 and d2xdy2
View SolutionIn dydx,x is a independent variable and y is the dependent variable. If independent and dependent variables are interchanged dydx becomes dxdy and these two are connected by the relation dydx.dxdy=1 . Find a relation between d2ydx2andd2xdy2 .
View SolutionIf p=dydx then d2ydx2=
View SolutionSolve d2ydx2=(dydx)2
View SolutionSolution of y(dydx)2+2xdydx=y is
View Solutiona(xdydx+2y)=xydydx
View SolutionFind order and degree 2x2d2ydx2−3dydx+y=0
View Solutionxd2ydx2+dydx+x=0
View SolutionThe solution of the equation y−xdydx=a(y2+dydx)is
View SolutionFind the order and degree of 2x2d2ydx2−3dydx+y=0
View Solution