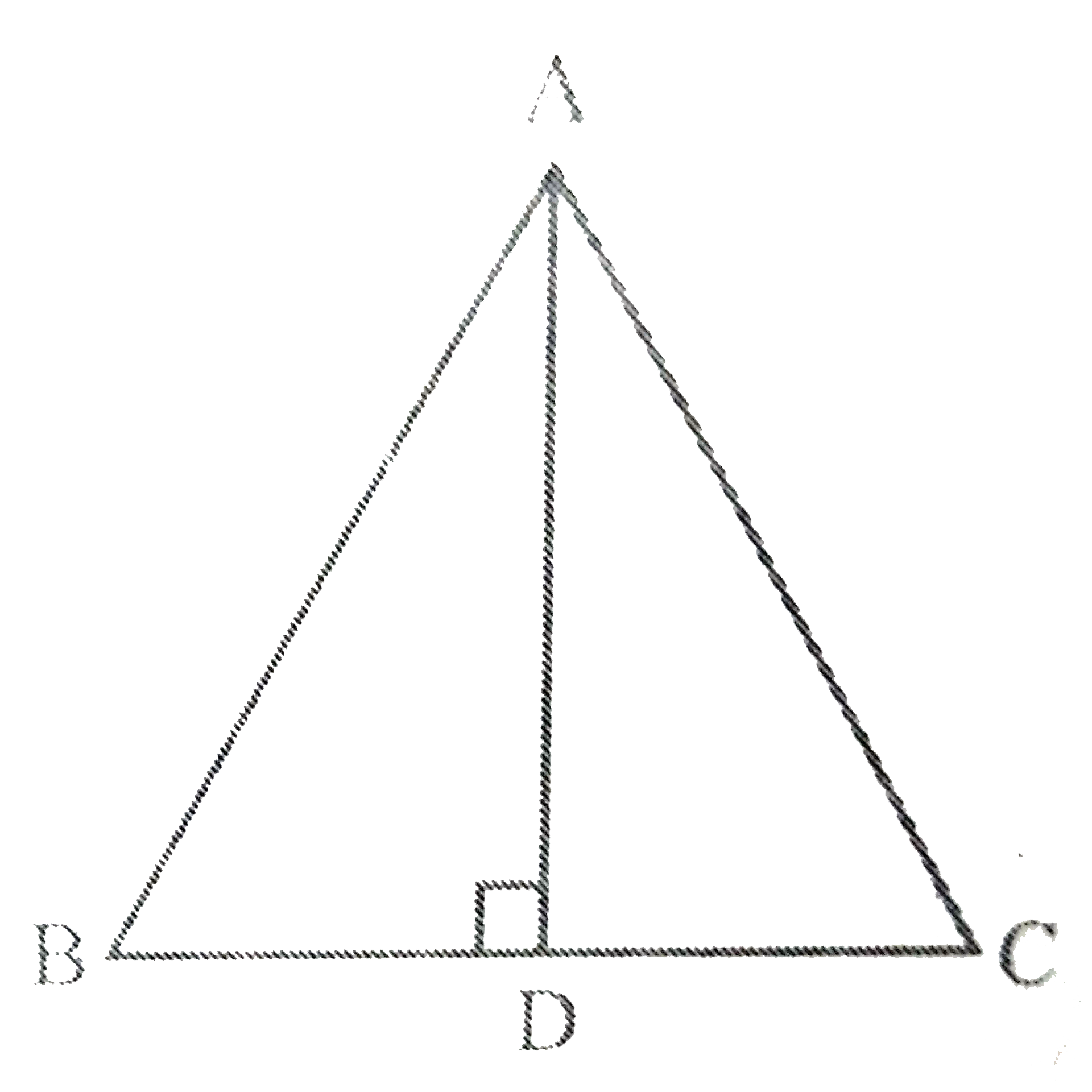
In , AD is the perpendicular bisector of BC (see Fig. 7.30). Show that is an isosceles triangle in which .
The correct Answer is:AC
Step by step video solution for In DeltaA B C, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that DeltaA B Cis an isosceles triangle in which A B\ =\ A C. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:EXERCISE 7.3
Explore 5 Videos
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:EXERCISE 7.4
Explore 6 Videos
- TRIANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIANGLESExercise:SUMS TO ENRICH REMEMBER
Explore 9 Videos
- SURFACE AREAS AND VOLUMESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SURFACE AREAS AND VOLUMESExercise:MULTIPLE CHOICE QUESTIONS
Explore 18 Videos
Similar Questions
Knowledge Check
In a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
A10B12C14D√221
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD
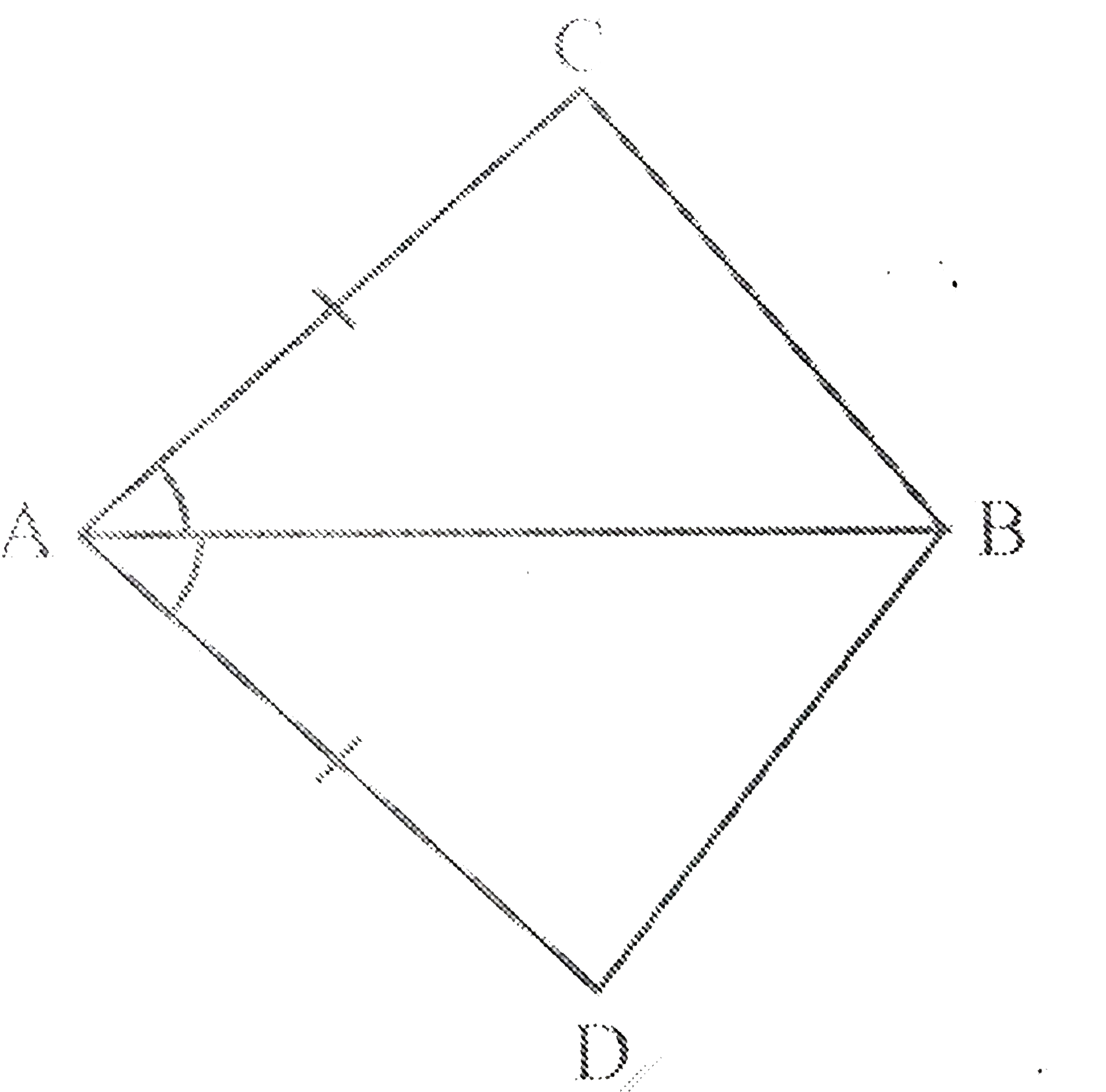
View SolutionIn ⋀ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
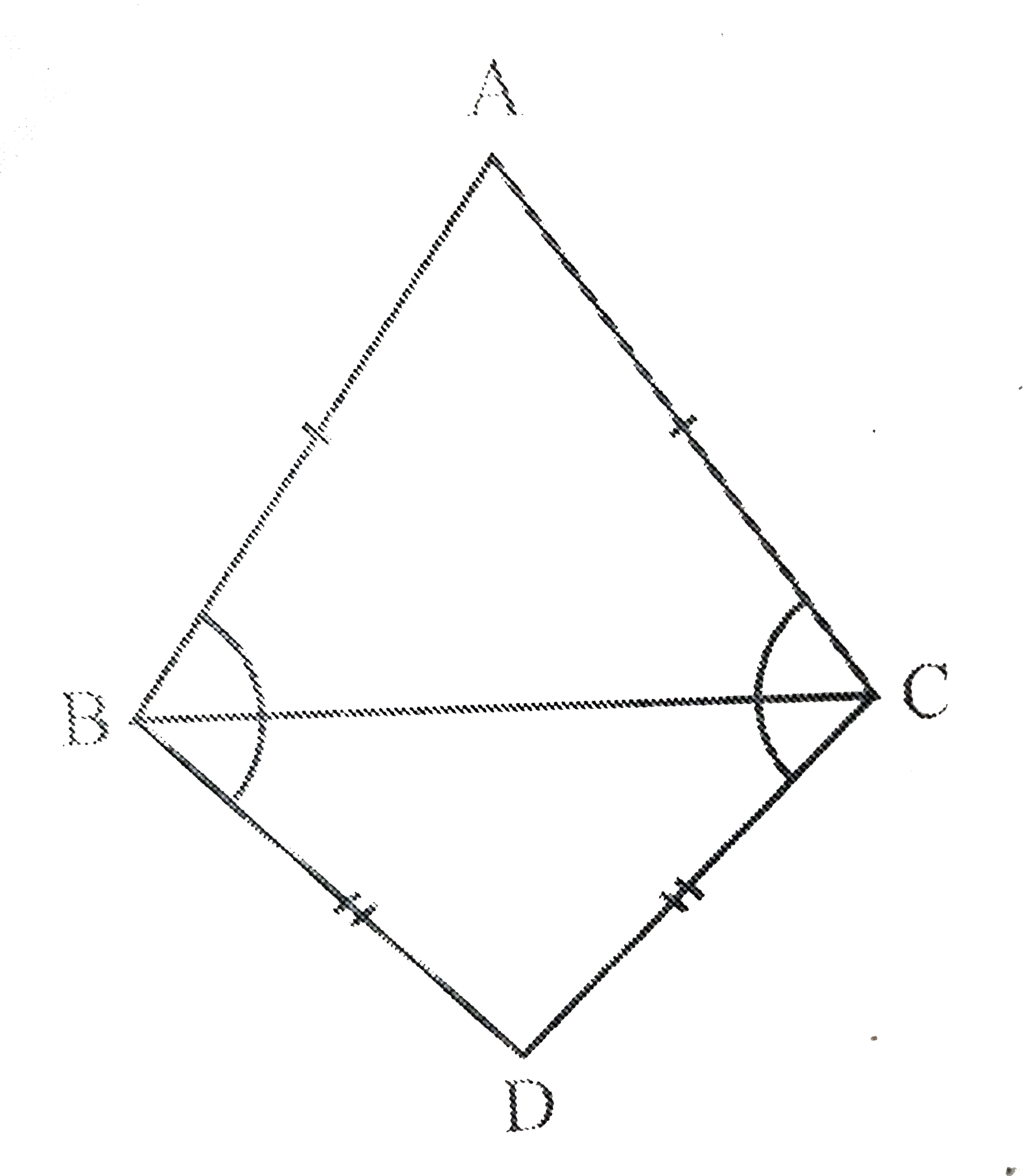
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
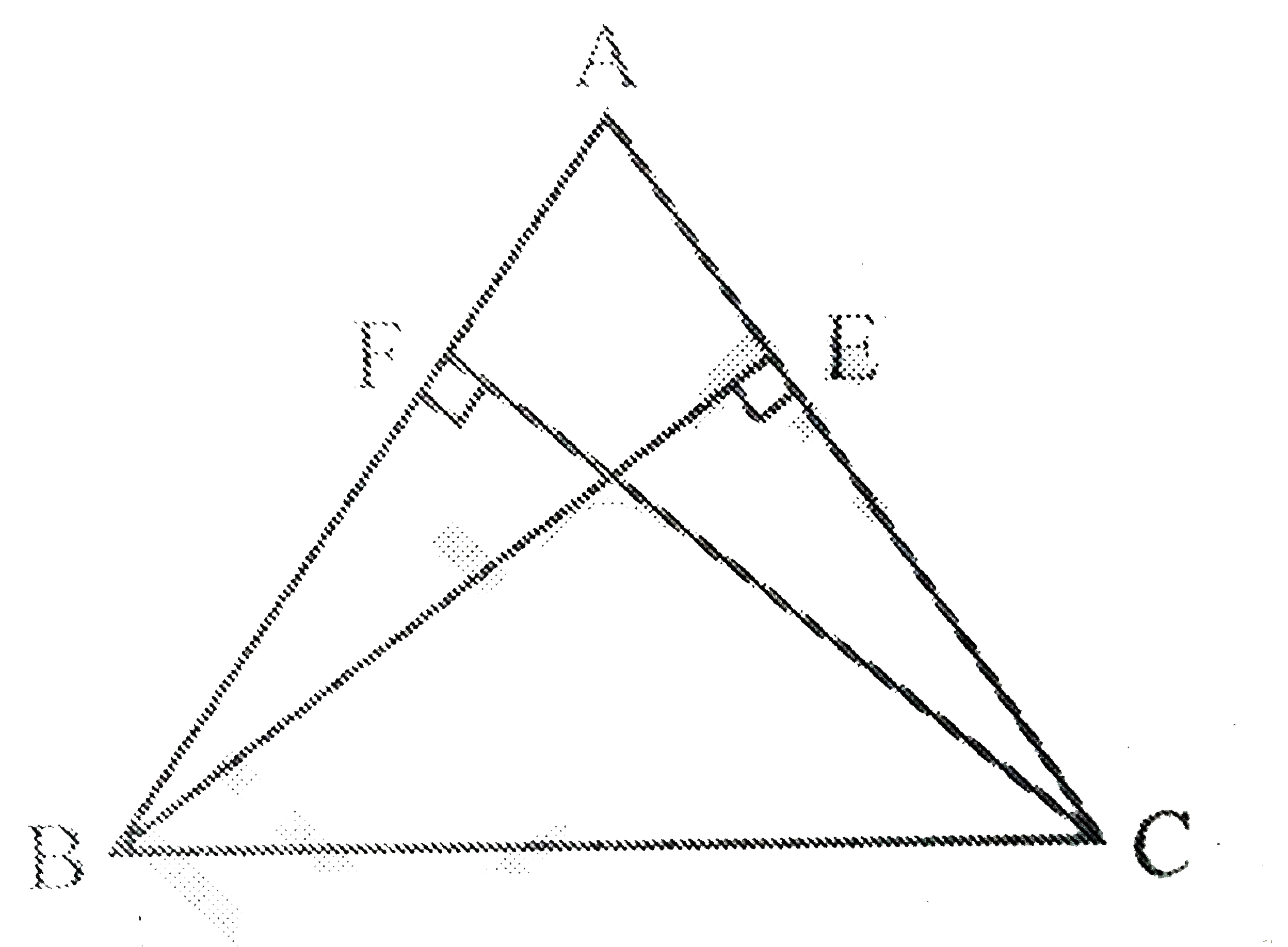
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View Solution