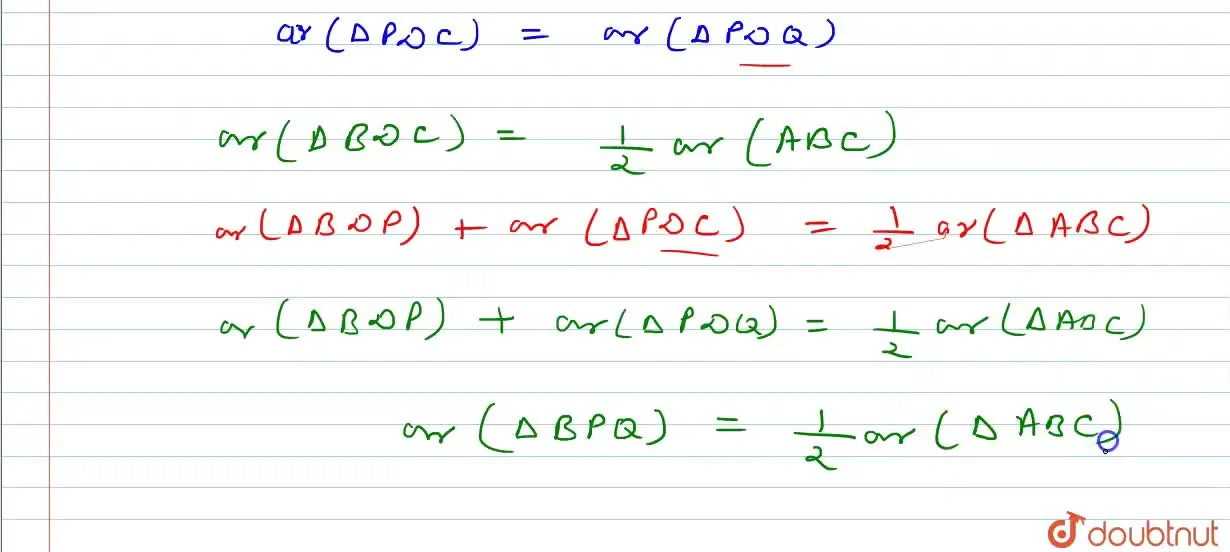In ABC, D is the mid-point of AB and P is any point on BC. If meets AB and Q (shown in figure), then prove that
.

Given In ABC, D is the mid-point of AB and P is any point on BC.
means AB in Q.
To prove
Construction Join PQ and CD.
Proof Since, D is the mid - point of AB. So CD is the median of .
We know that, a median of a triangle divides it into two triangles of equal areas.

...(i)
Now, and are on the same base DP and between the same parallel lines DP andCQ.
So, ...(ii)
On putting the value from Eq. (ii) in Eq. (i), we get
Hence proved.
Related Playlists
Similar Questions
In the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
 View Solution
View SolutionIn the given figure, in △ABC, D is the mid-point cf AB and P is any point on BC. If CQ∣∣PD meets AB in Q and area of △ABC=30cm2, then, area of △BPQ is
View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View Solutionin figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View Solutionin figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
 View Solution
View SolutionIn figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
 View Solution
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View Solution