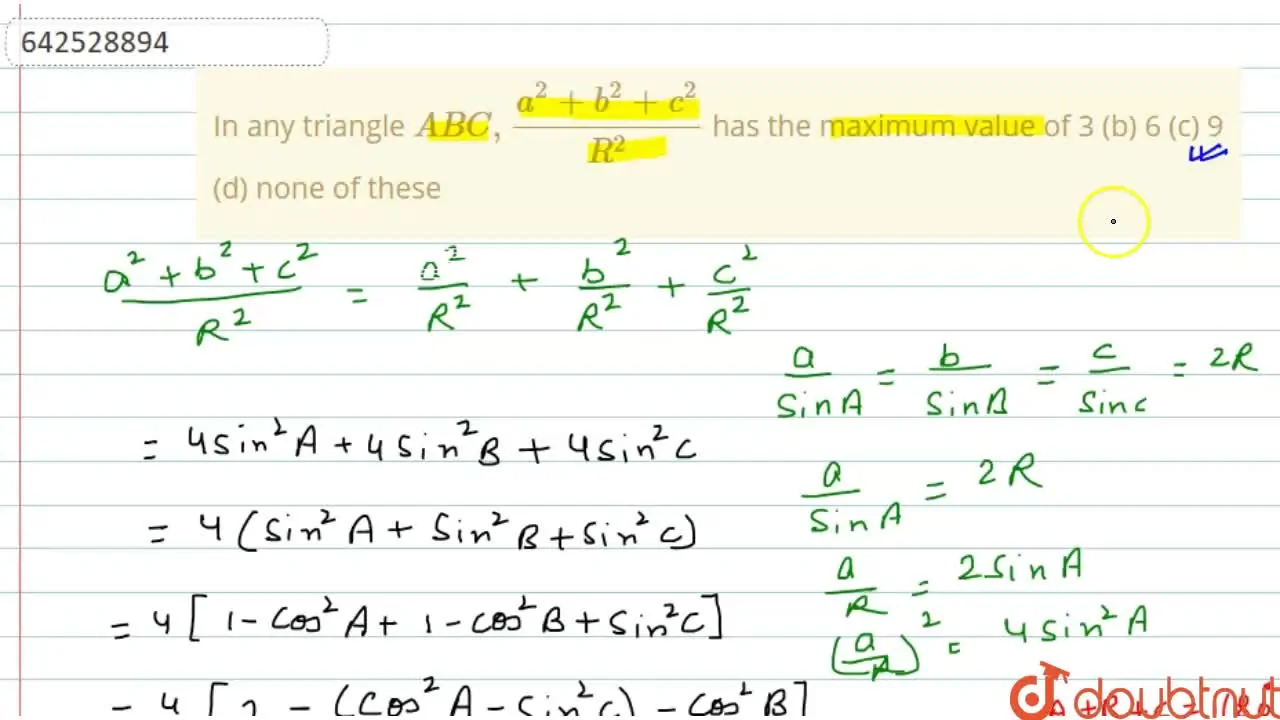
In any triangle ABC,a2+b2+c2R2 has the maximum value of 3 (b) 6 (c) 9 (d) none of these
a2+b2+c2R2=(2RsinA)2+(2RsinB)2+(2Rsinc)2R2
4(sin2A+sin2B+sin2C)
4⋅2(1+cosAcosBcosC)
8(1+cosAcosBcosC)
8(1+18)
8(98)
9
Option C is correct.
Related Playlists
Similar Questions
In any triangle, the minimum value of r1r2r3/r3 is equal to (a) 1 (b) 9 (c) 27 (d) none of these
View SolutionIn TriangleABC with fixed length of BC, the internal bisector of angle C meets the side ABatD and the circumcircle at E . The maximum value of CD×DE is c2 (b) c22 (c) c24 (d) none of these
View SolutionIn any triangle ABC, the least valeu of sin2A+sinA+1sinAis(A)3(B)√3 (C) 9 (D) none of these
View SolutionStatement - I : In any triangle ABC , the minimum values of r1+r2+r3r is 9 Because : Statement - II : For any three number AM≥GM A (b) B (c) C (d) D
View SolutionIn triangle ABC,b2sin2C+c2sin2B=2bcwhereb=20,c=21, then inradius= (a) 4 (b) 6 (c) 8 (d) 9
View SolutionIn any triangle ABC, prove that:Δ=b2+c2−a24cotA .
View SolutionIn any triangle ABC, if sin A , sin B, sin C are in AP, then the maximum value of tanB2 is
View SolutionIf a+b+c=9 and ab+bc+ca=23 , then a2+b2+c2=?
(a)35
(b) 58
(c) 127
(d) none of theseView SolutionIn a triangle ABC, (a2−b2−c2)tanA+(a2−b2+c2)tanB is equal to(a) (a2+b2−c2)tanC (b) (a2+b2+c2)tanC (b2+c2−a2)tanC (d) none of these
View SolutionIf a2=b3=c4, then a:b:c=
(a) 2:3:4
(b) 4:3:2
(c) 3:2:4
(d) None of theseView Solution