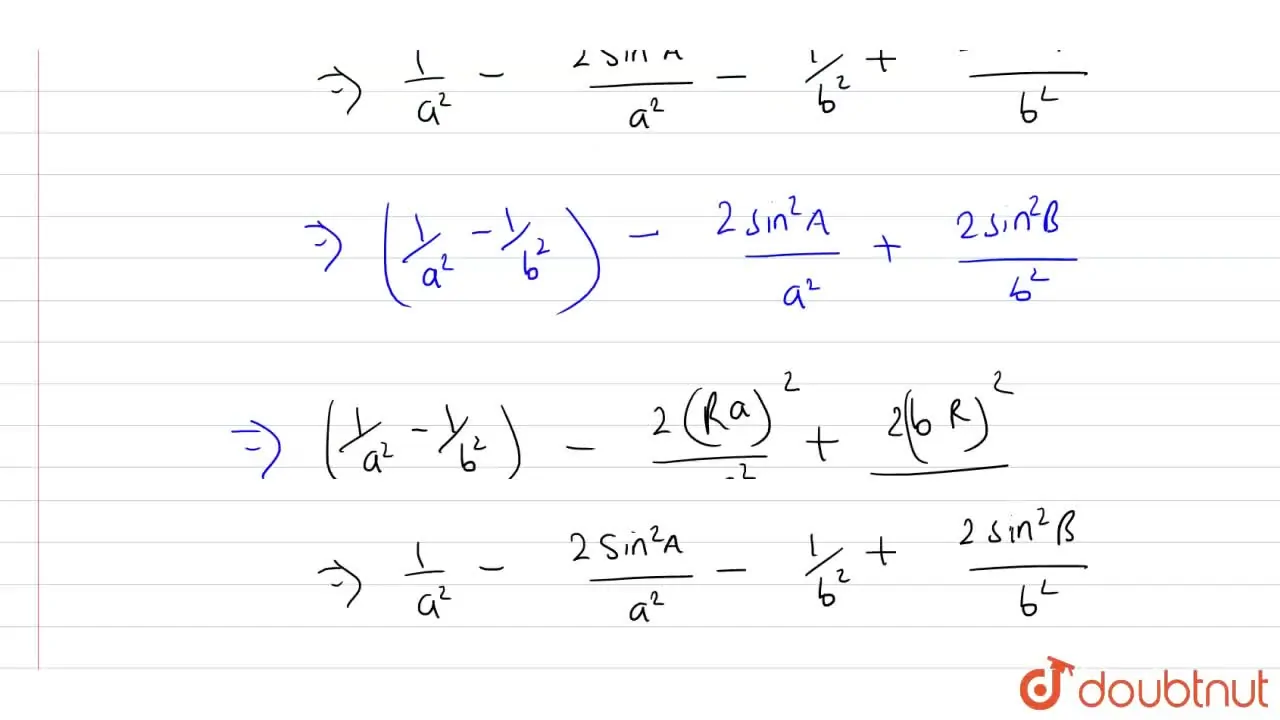In any ΔABC, prove that
cos2Aa2−cos2Bb2=(1a2−1b2)
Video Solution
Text Solution
LHS=(1−2sin2A)a2−(1−2sin2B)b2=(1a2−1b2)−2sin2Aa2+2sin2Bb2
=(1a2−1b2)−2sin2Ak2sin2A+2sin2Bk2sin2B
=(1a2−1b2)−2k2+2k2=(1a2−1b2).
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - EXERCISE 18 B3videos
SOLUTION OF TRIANGLES
- BOOK - RS AGGARWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - EXAMPLE (Problems Based on Sine Cosine Formulae)5videos
SOLUTION OF TRIANGLES
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - EXERCISE-1H15videos
SETS
- BOOK - RS AGGARWALCHAPTER - SOME SPECIAL SERIESEXERCISE - EXERCISE 13B (Very short Answer Questions)9videos
SOME SPECIAL SERIES
Similar Questions
cos(2A)a2−cos(2B)b2=1a2−1b2
View SolutionIn any ΔABC, prove that : a2(cos2B−cos2C)+b2(cos2C−cos2A)+c2(cos2A−cos2B)=0
View SolutionIn any ΔABC, prove that : a(bcosC−ccosB)=b2−c2.
View SolutionIn any ΔABC, prove that : (b2−c2)cos2A+(c2−a2)cos2B+(a2−b2)cos2C=0
View SolutionIn any ΔABC, prove that: cosAa+cosBb+cosCc=a2+b2+c22abc
View SolutionIn any ΔABC, prove that : cos2(A2)a+cos2(B2)b+cos2(C2)c=s3abc
View SolutionIn ΔABC, prove that:
(b+c)cos(B+C)2=acos(B−C)2View SolutionIn any ΔABC, prove that : 1+cos(A−B)cosC1+cos(A−C)cosB=a2+b2a2+c2
View SolutionIn ΔABC, prove that:
a(cos2C3−cos2B2)=(b−c).cos2A2View SolutionIn any ΔABC, prove that (a−b)2cos2C2+(a+b)2sin2C2=c2.
View Solution