In a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
Video Solution
Text Solution
N/a
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IVOne of the corner points of the feasible region of inequalities gives
AOptimal solution of LPPBObjective functionCConstraintsDLinear assumptions
Define a corner point of a feasible region.
View SolutionThe maximum value of objective function Z=3x+y under given feasible region is
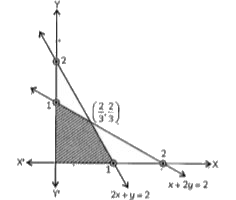
View SolutionIn a LPP, the objective function is always.
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
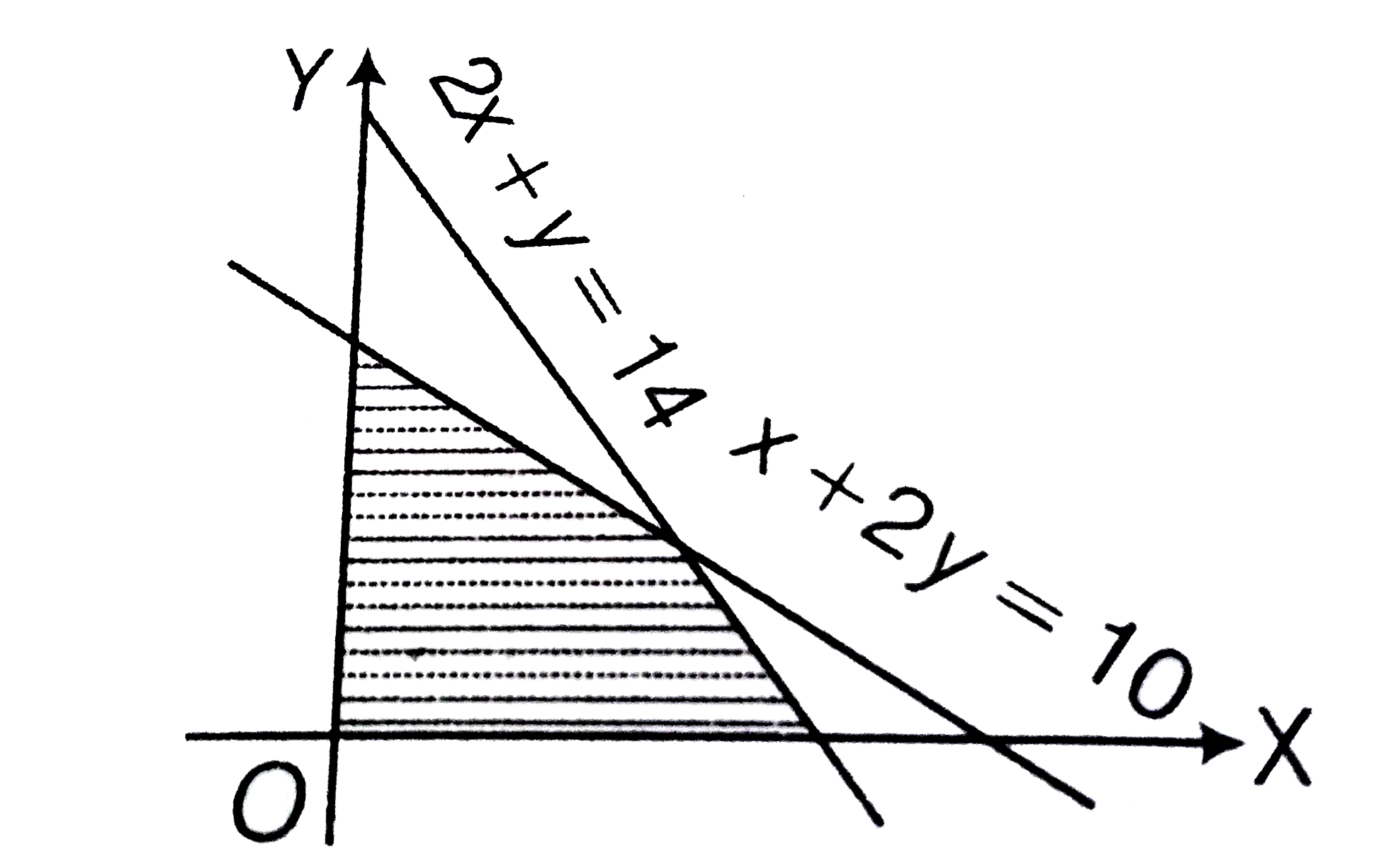
View SolutionThe, objective function is maximum or minimum at a point, which lies on the boundary of the feasible region.
View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View Solution

