In a circle of radius r, chords of length aandbcm subtend angles θand3θ , respectively, at the center. Show that r=a√a3a−bcm
To solve the problem, we need to show that in a circle of radius r, where chords of lengths a and b subtend angles θ and 3θ at the center, the relationship r=a√a3a−b holds.
1. Identify the triangles:
We have two triangles formed by the radius and the chords:
- Triangle OAB for chord AB with length a subtending angle θ.
- Triangle OBC for chord BC with length b subtending angle 3θ.
2. Apply the cosine rule in triangle OAB:
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(θ)
Since OA=OB=r (the radius),
a2=r2+r2−2r2cos(θ)
Simplifying gives:
a2=2r2(1−cos(θ))
3. Use the identity for 1−cos(θ):
We can express 1−cos(θ) using the sine function:
1−cos(θ)=2sin2(θ2)
Substituting this into the equation gives:
a2=2r2⋅2sin2(θ2)=4r2sin2(θ2)
Rearranging gives:
r=a2sin(θ2)
4. Apply the cosine rule in triangle OBC:
Similarly, for triangle OBC:
BC2=OB2+OC2−2⋅OB⋅OC⋅cos(3θ)
Again, since OB=OC=r:
b2=r2+r2−2r2cos(3θ)
Simplifying gives:
b2=2r2(1−cos(3θ))
5. Use the identity for 1−cos(3θ):
We can express 1−cos(3θ) using the sine function:
1−cos(3θ)=2sin2(3θ2)
Substituting this into the equation gives:
b2=2r2⋅2sin2(3θ2)=4r2sin2(3θ2)
Rearranging gives:
r=b2sin(3θ2)
6. Relate the two expressions for r:
We have two expressions for r:
r=a2sin(θ2)andr=b2sin(3θ2)
Setting them equal gives:
a2sin(θ2)=b2sin(3θ2)
Cross-multiplying gives:
asin(3θ2)=bsin(θ2)
7. Use the sine triple angle formula:
The sine triple angle formula states:
sin(3θ)=3sin(θ)−4sin3(θ)
We can express sin(3θ2) in terms of sin(θ2) and substitute back.
8. Final expression for r:
After simplifying, we arrive at:
r=a√a3a−b
We have two triangles formed by the radius and the chords:
- Triangle OAB for chord AB with length a subtending angle θ.
- Triangle OBC for chord BC with length b subtending angle 3θ.
AB2=OA2+OB2−2⋅OA⋅OB⋅cos(θ)
Since OA=OB=r (the radius),
a2=r2+r2−2r2cos(θ)
Simplifying gives:
a2=2r2(1−cos(θ))
We can express 1−cos(θ) using the sine function:
1−cos(θ)=2sin2(θ2)
Substituting this into the equation gives:
a2=2r2⋅2sin2(θ2)=4r2sin2(θ2)
Rearranging gives:
r=a2sin(θ2)
Similarly, for triangle OBC:
BC2=OB2+OC2−2⋅OB⋅OC⋅cos(3θ)
Again, since OB=OC=r:
b2=r2+r2−2r2cos(3θ)
Simplifying gives:
b2=2r2(1−cos(3θ))
We can express 1−cos(3θ) using the sine function:
1−cos(3θ)=2sin2(3θ2)
Substituting this into the equation gives:
b2=2r2⋅2sin2(3θ2)=4r2sin2(3θ2)
Rearranging gives:
r=b2sin(3θ2)
We have two expressions for r:
r=a2sin(θ2)andr=b2sin(3θ2)
Setting them equal gives:
a2sin(θ2)=b2sin(3θ2)
Cross-multiplying gives:
asin(3θ2)=bsin(θ2)
The sine triple angle formula states:
sin(3θ)=3sin(θ)−4sin3(θ)
We can express sin(3θ2) in terms of sin(θ2) and substitute back.
After simplifying, we arrive at:
r=a√a3a−b
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Illustration
Explore 86 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.1
Explore 12 Videos
- PROGRESSION AND SERIESBook:CENGAGE ENGLISHChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Archives(Matrix Match Type)
Explore 1 Video
Similar Questions
Two parallel chords are drawn on the same side of the centre of a circle of radius R. It is found that they subtend and angle of θ and 2θ at the centre of the circle. The perpendicular distance between the chords is
View SolutionIf arcs of same length in two circles subtend angles of 600and750 at their centers, find the ratios of their radii.
View SolutionIf arcs of same length in two circles subtend angles of 600and750 at their centers, find the ratios of their radii.
View SolutionA circle of radius r cm has a diameter of length
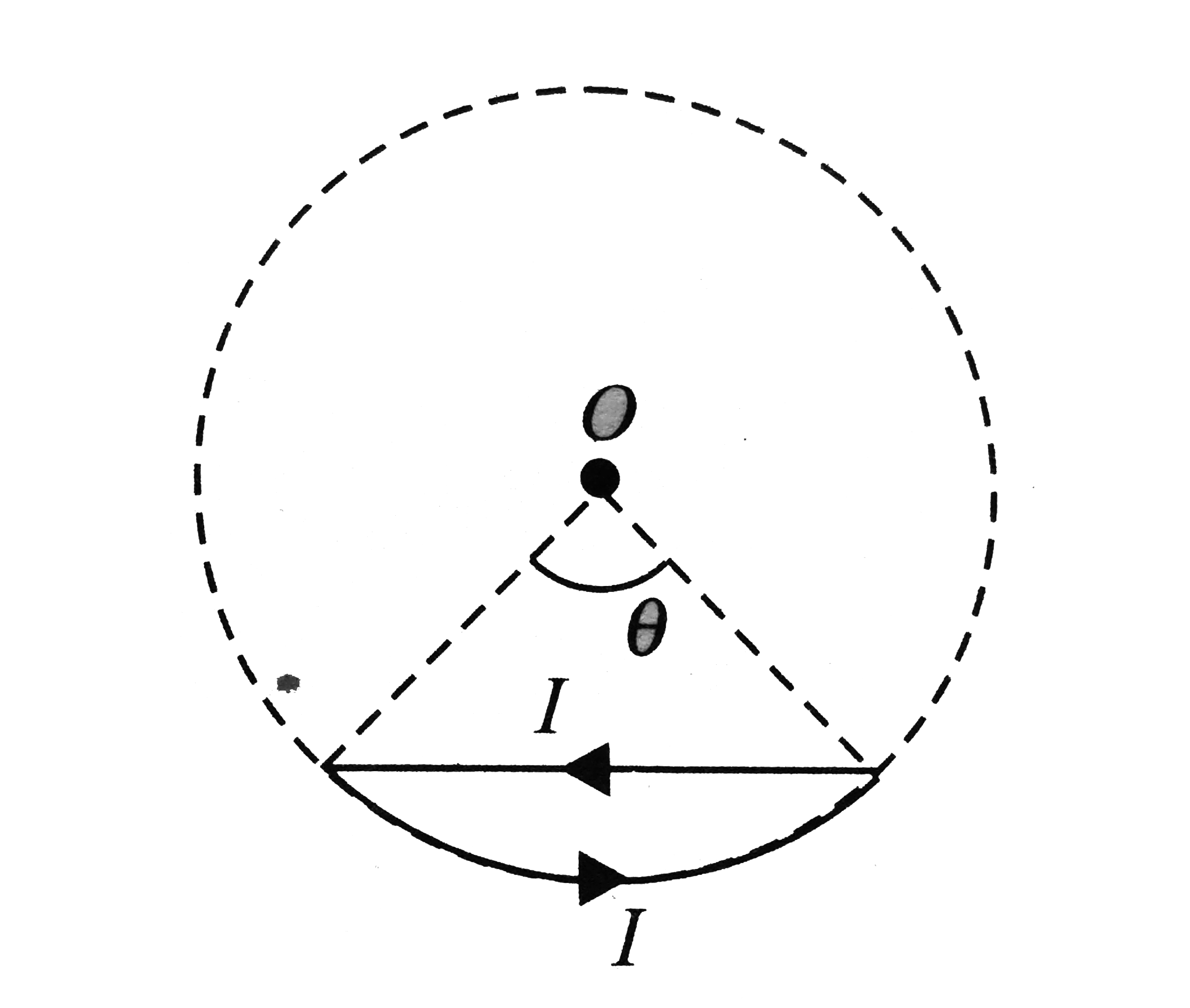
View SolutionFigure. Shows a small loop carrying a current I. The curved portion is an arc of a circle of radius R and the straight portion is a chord to the same circle subtending an angle θ. The magnetic induction at centor O is
View SolutionLet PQ and RS be two parallel chords of a given circle of radius 6 cm, lying on the same side of the center. If the chords subtends angles of 72∘and 144∘ at the center and the distance between the chords is d, then d2 is equal to
View SolutionThe locus of the mid-points of the chords of the circle of lines radiùs r which subtend an angle π4 at any point on the circumference of the circle is a concentric circle with radius equal to (a) r2 (b) 2r3 (c) r√2 (d) r√3
View SolutionTwo equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circles is √r (b) √2 r AB (c) √3 r (d) √32 r
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC.
View SolutionIf a chord AB of a circle subtends an angle θ(≠π/3) at a point C on the circumference such that the triangle ABC has maximum area , then
View Solution

