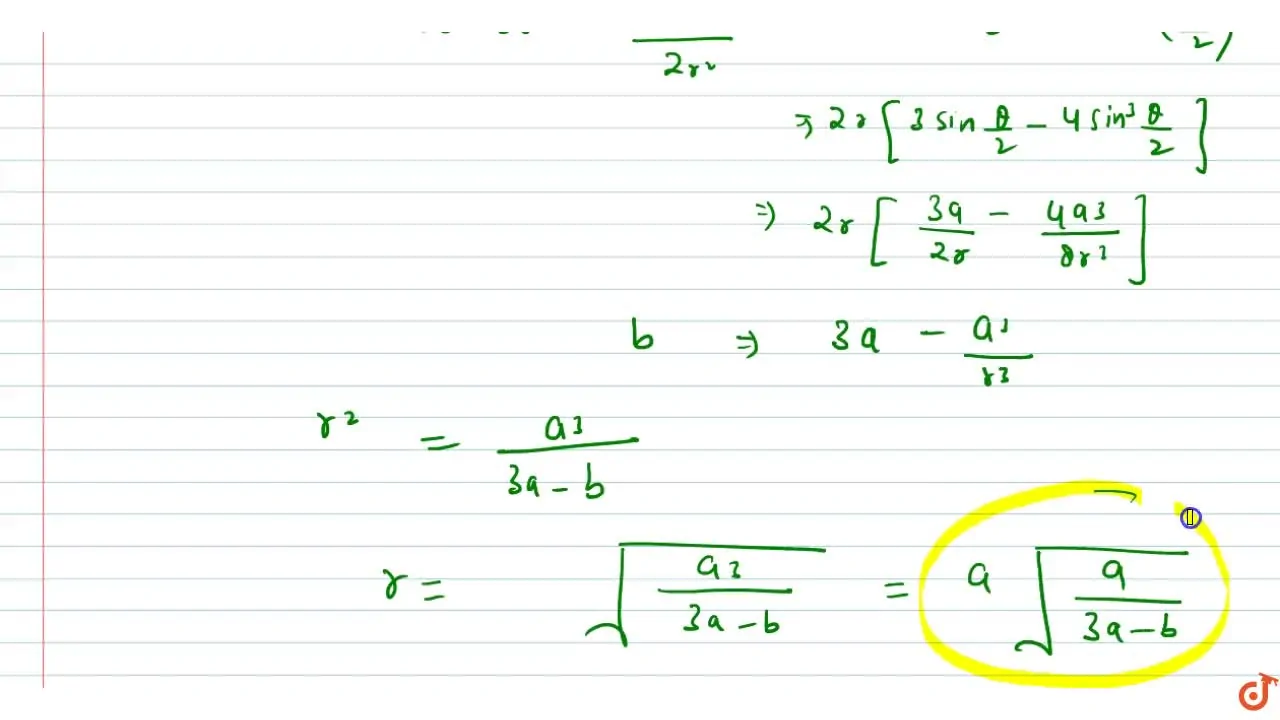In a circle of radius r, chords of length aandbcm subtend angles θand3θ , respectively, at the center. Show that r=a√a3a−bcm
We can create a diagram with the given details.
Please refer to video for the diagram.
Now, in ΔOAB,
cosθ=r2+r2−a22⋅r⋅r=2r2−a22r2
⇒cosθ=1−a22r2
⇒a22r2=1−cosθ=2sin2(θ2)
⇒a=2rsin(θ2)→(1)
Now, in ΔOCB,
cos3θ=r2+r2−b22⋅r⋅r=2r2−b22r2
⇒b=2rsin(3θ2)
⇒b=2r(3sin(θ2)−4sin3(θ2))
From (1),
⇒b=2r(3(a2r)−4(a3)8r3)
⇒b=3a−a3r2
⇒r2=a33a−b
⇒r=a√a3a−bcm
Related Playlists
Similar Questions
In a circle of radius r, chords of length aandbcm subtend angles θand3θ , respectively, at the center. Show that r=a√a3a−bcm
View SolutionConsider a circle of radius R. What is the lengths of a chord which subtends an angle θ at the centre ?
View SolutionConsider a circle of radius R. What is the lengths of a chord which subtends an angle θ at the centre ?
View SolutionTwo parallel chords are drawn on the same side of the centre of a circle of radius R. It is fouind that they subtend angles of θ and 2θ at the centre of the circle. The prependicular distance between the chords is
View SolutionLet p and q be the length of two chords of a circle which subtend angles 36∘and60∘ respectively at the centre of the circle . Then , the angle (in radian) subtended by the chord of length p + q at the centre of the circle is (use π=3.1 )
View SolutionTwo parallel chords are drawn on the same side of the centre of a circle of radius R. It is found that they subtend and angle of θ and 2θ at the centre of the circle. The perpendicular distance between the chords is
View SolutionIf a semi perimeter of a circle of radiÂus r equals perimeter of a sector of the same circle subtending and angle θ at the center then,
View SolutionWhat is the area of a segment of a circle of radius r subtending an angle θ at the centre ?
View SolutionDraw a circle with radius 3.4 cm. Draw a chord MN of length 5.7cm in it. Construct tangents at points M and N to the circle.
View SolutionTwo chords of length 'a' meter and 'b' meter make an angle of 60∘and90∘ at the centre of circle. Which of the following option are correct-
View Solution