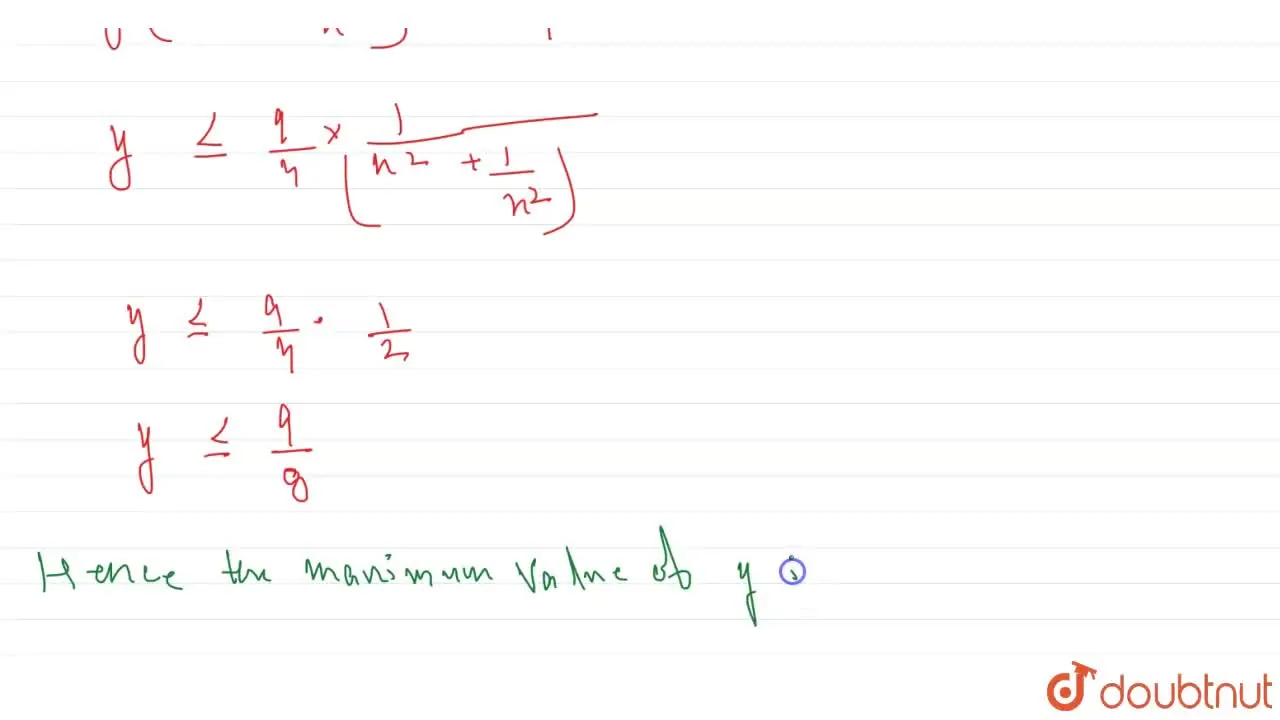In ABC Prove that cos2A2+cos2B2+cos2C2≤94. If cos2A2+cos2B2+cos2C2=y(x2+1x2) then find the maximum value of y.
Step by step video & image solution for In A B C Prove that cos^2A/2+cos^2B/2+cos^2C/2lt=9/4dot If cos^2A/2+cos^2B/2+cos^2C/2=y(x^2+1/(x^2)) then find the maximum value of ydot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
Prove that (cos2A−sin2B)+1−cos2C
View SolutionIn a △ABCcos2A2+cos2B2+cos2C2=
View SolutionIn ABC, prove that (a−b)2cos2C2+(a+b)2sin2C2=c2.
View SolutionIn ABC, prove that (a−b2cos2C2+(a+b)2sin2C2=c2.
View SolutionIf A+B+C=1800, prove that : cos2(A2)+cos2(B2)−cos2(C2)=2cos(A2)cos(B2)sin(C2)
View SolutionIn any ABC , prove that: 2{bcos2(C2)+ccos2(B2)}=a+c+b
View SolutionIn ΔABC, prove that:
cos2A+cos2B−cos2C=1−4sinAsinBcosCView SolutionProve that: cos2A+cos2B−2cosA cosBcos (A+B)=sin2(A+B)
View SolutionProve that: cos2A+cos2B−2cosA cosBcos (A+B)=sin2(A+B)
View SolutionIn ABC, prove that cosecA2+cosecB2+cosecC2≥6.
View Solution