P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
(i)From APQ we have,
ar.(APQ)
=½⋅(12)ar.(ABQ)
=(12)⋅(12)⋅(12)ar.(ABC)
=(18)ar.(ABC)————–(1)
Similarly from,v
ar.(ARC)=(12)(APC)v
=(12)⋅(12)ar.(ABC)
=(14)ar.(ABC)—————(2)v
So,From equation (1)
ar.(PRQ)=(18)ar.(ABC)
=(12)⋅1(/4)ar.(ABC)——–[om2]
(ii) ar(ABC)+ar.(ARQ)−ar(ARC)——1
From AQC,
ar(AQC)=(12)(ABC)
ar.(ABC)=(12)ar.(APQ)
=(12)ar.(ABQ)
=(12)⋅(12)⋅(12)ar.(ABC)
=(18)ar.(ABC)
And,ar.(ARC)=(12)ar.(APC)
=12ar.(ABC)
And,ar.(RQC)=ar.(AQC)+ar.(ARQ)+ar.(ARC)
=(12)ar.(ABC)+(18)ar.(ABC)−14ar.(ABC)
=(12+18−14)ar.(ABC)
=(4+1−28)ar.(ABC)
=(5−28)ar.(ABC)
=(38)ar.(ABC)
(iii)
From,ar(PBQ)=12ar.(ABQ)
=12⋅12ar.(ABC)
=14ar.(ABC)——–(1)
And,ar.(ARC)=12ar.(APC)
=12⋅12ar.(ABC)
=14ar.(ABC)——(2)
Form 1 and 2
ar.(PBQ)=ar.(ARC)
Topper's Solved these Questions
Similar Questions
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionP, Q and R are, respectively, the mid points of sides BC, CA and AB of a triangle ABC and AD is the perpendicular from vertex A to BC,then prove that the points P,Q,R and D are cyclic.
View SolutionIf P, Q, R are the mid-points of the sides AB, BC and CA respectively of a triangle ABC and a, p, q are the position vectors of A,P,Q respectively, then what is position vector of R?
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
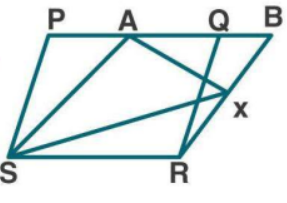 View Solution
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution
