If z is a complex number satisfying |z|2+2(z+2)+3i(z−¯z)+4=0, then complex number z+3+2i lies on
circle witih center 1-5i and radius 4
circle with center 1+5i and radius 4
circle with center 1+5i and radius 3
circle with center 1-5i and radius 3
The correct Answer is:B
We have,
|z|2+2(z+¯z)+3i(z−¯z)+4=0
⇒z¯z+(2+3i)z+(2−3i)¯z+4=0
Clearly, it represents a circle with centers as (−2,3) and radius =√4+9−4=3.
The above equation can be written as
|z−(2+3i)|=4 or , |z+2−3i|=4⇒|ω−3−2i+2−3i|=4⇒|ω−1−5i|=4
⇒ω lies on the circle with center 1+5i and radius 4.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type15videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise131videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
z is a complex number satisfying z4+z3+2z2+z+1=0, then |z| is equal to
View Solutionz is a complex number satisfying z4+z3+2z2+z+1=0, then |z| is equal to
View SolutionNumber of complex numbers satisfying z3=¯z is
View SolutionIf z=x+iy is a complex number satisfying ∣∣∣z+i2∣∣∣2=∣∣∣z−i2∣∣∣2 , then the locus of z is
View SolutionIf z=x+iy is a complex number satisfying ∣∣∣z+i2∣∣∣2=∣∣∣z−i2∣∣∣2 , then the locus of z is
View SolutionLet z be a complex number satisfying |z|3+2z2+4¯z−8=0 , where ¯z denotes the complex conjugate of z . Let the imaginary part of z be nonzero
Match each entry in List-I to the correct entries in List-II.
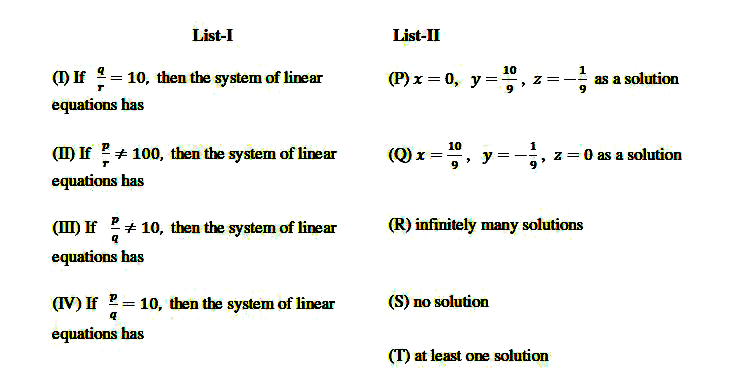
The correct option is:View SolutionIf z is a complex number satisfying z4+z3+2z2+z+1=0 then the set of possible values of z is
View SolutionIf z is a complex number satisfying z4+z3+2z2+z+1=0 then the set of possible values of z is
View SolutionIf z is a complex number satisfying z4+z3+2z2+z+1=0 then the set of possible values of z is
View SolutionLet z be a complex number satisfying (3+2i) z+(5i-4) ¯z=-11-7i .Then |z|2 is
View Solution

