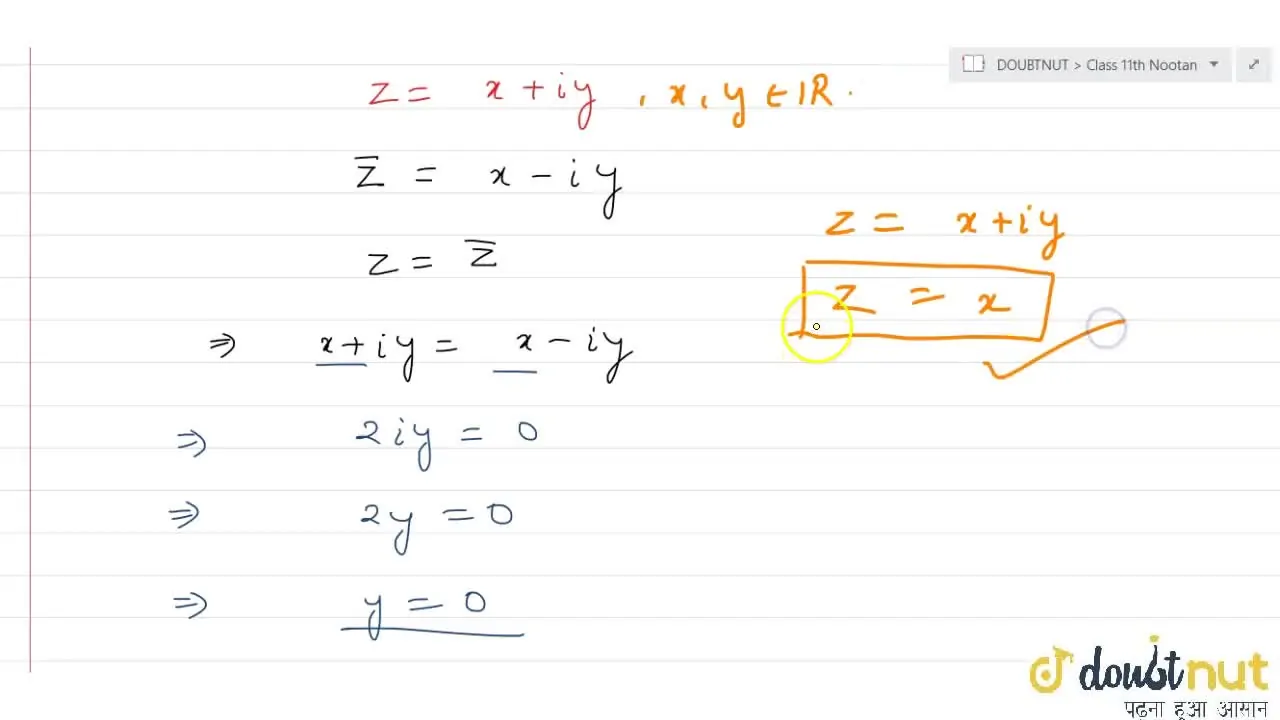If z is a complex number and z=¯z, then prove that z is a purely real number.
The correct Answer is:N/a
Let z=x+iy
⇒ ¯z=x−iy
Now, z=¯z
⇒ x+iy=x−iy
⇒ 2iy=0
⇒ y=0
∴ z=x+iy
=x
⇒z is purely real number. Hence proved.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - EXERCISE 5A9videos
COMPLEX NUMBERS AND QUADRATIC EQUATION
- BOOK - NAGEEN PRAKASHANCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - EXERCISE 5B28videos
COMPLEX NUMBERS AND QUADRATIC EQUATION
- BOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Example68videos
BINOMIAL THEOREM
- BOOK - NAGEEN PRAKASHANCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Exercise8videos
CONIC SECTION
Similar Questions
If z is a complex number such that Re(z)=Im(z), then
View SolutionIf z is a complex number such that z+i|z|=i¯z+1 ,then |z|is -
View SolutionIf z is a complex number such that Re (z) = Im (z), then
View SolutionIf ∣∣∣z|¯z|−¯z∣∣∣=1+|z|, then prove that z is a purely imaginary number.
View SolutionIf z is a complex number, then (¯z−1)(¯z) is equal to
View SolutionIf z is a complex number such that |z|=1, prove that z−1z+1 is purely imaginary, what will by your conclusion if z=1?
View SolutionIf 2 = 1 + ai is a complex number, a>0, such that z3 is a real number. Then the value of the sum 1+z+z2+……+z11 is equal to,
View SolutionLet z≠i be any complex number such that z−iz+i is a purely imaginary number. Then z+1z is
View SolutionProve that for any complex number z, the product z¯z is always a non-negative real number.
View SolutionIf z is a complex number such taht z2=(¯z)2, then find the location of z on the Argand plane.
View Solution