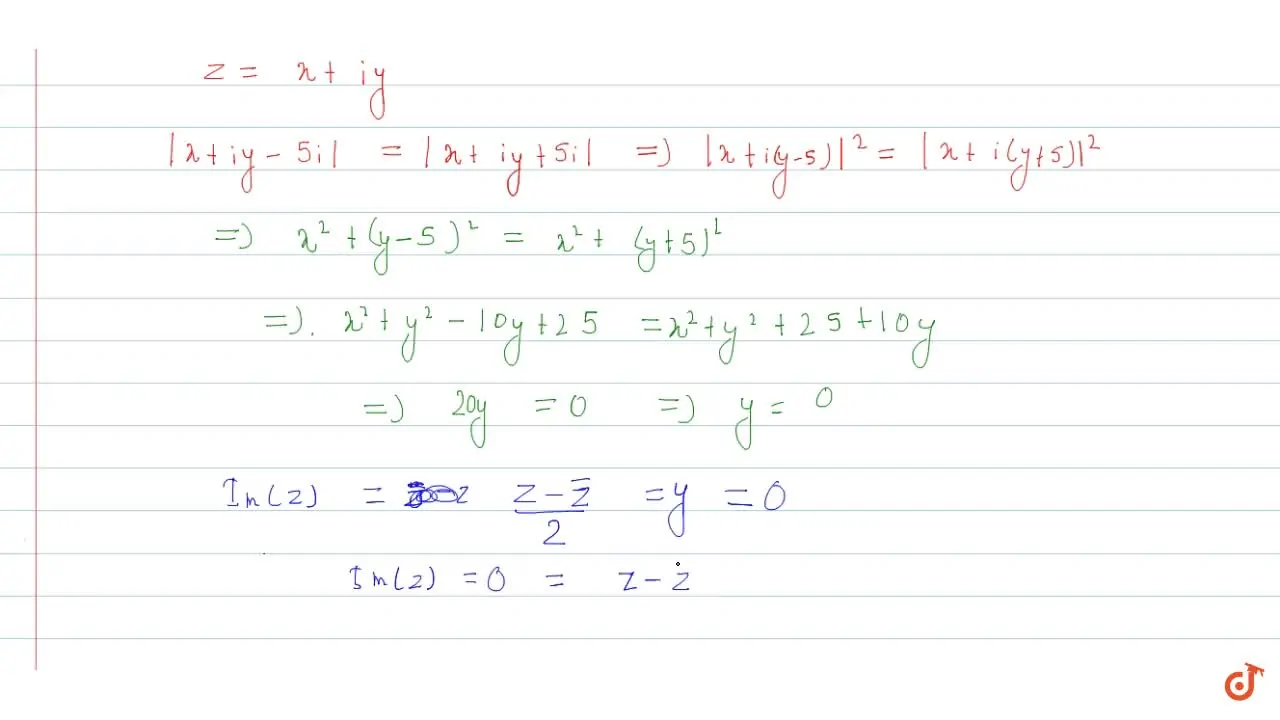If |z−5i|=∣z+5i , then the locus of z.
Video Solution
Text Solution
Let z=x+iy
Then,
|x+iy−5i|=|x+iy+5i|
⇒|x+(y−5)i|=|x+(y+5)i|
⇒x2+(y−5)2=x2+(y+5)2
⇒−10y=10y
⇒−20y=0
⇒y=0
So, imaginary part of z is 0.
We can write it as,
z−¯z2=0
z−¯z=0, which is the required locus.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If |z−3i|=|z+3i|, then find the locus of z.
View SolutionIf |z−1−i|=1, then the locus of a point represented by the complex number 5(z−i)−6 is
View SolutionIf |z+2+3i|=5 then the locus of z is
View SolutionIf |z+3i|+|z−i|=8, then the locus of z, in the Argand plane, is
View SolutionIf |z+i|2−|z−i|2=4 then the locus of z is
View SolutionIf |z+i|2−|z−i|2=3 then the locus of z is
View Solutionif |z−1|=|z−i| then locus of z is
View SolutionIf z satisfies |z−6+4i|+|z−3+2i|=13, then the locus of z is
View Solution|z+2+3i|=5 is the locus of
View SolutionIf Im(z−i2i)=0 then the locus of z is
View Solution