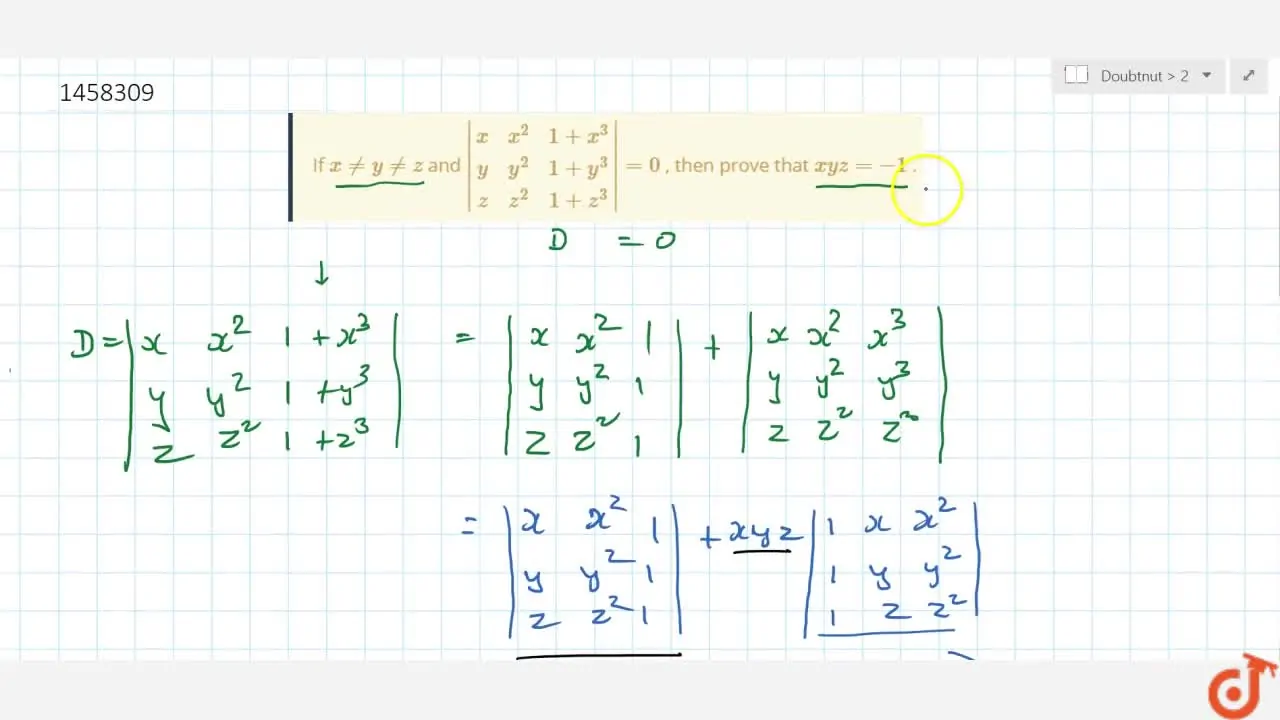
If x≠y≠z and ∣∣×21+x3yy21+y3zz21+z3∣∣=0 , then prove that xyz=−1 .
The correct Answer is:Proved
$$
\Delta=\left|\begin{array}{lll}
x & x^{2} & 1+x^{3} \\
y & y^{2} & 1+y^{3} \\
z & z^{2} & 1+z^{3}
\end{array}\right|=0
$$
Now, we know that If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants.
$$
\begin{aligned}
&\therefore \Delta=\left|\begin{array}{lll}
x & x^{2} & 1 \\
y & y^{2} & 1 \\
z & z^{2} & 1
\end{array}\right|+\left|\begin{array}{ccc}
x & x^{2} & x^{3} \\
y & y^{2} & y^{3} \\
z & z^{2} & z^{3}
\end{array}\right| \\
&=(-1)^{2}\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|+x y z\left|\begin{array}{ccc}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|
\end{aligned}
$$
(Using C3↔C2 and then C1↔C2 )
$$
\begin{aligned}
&=(1+x y z)\left|\begin{array}{ccc}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right| \\ \\
&=(1+x y z)\left|\begin{array}{ccc}
1 & x & x^{2} \\
0 & y-x & y^{2}-x^{2} \\
0 & z-x & z^{2}-x^{2}
\end{array}\right|
\end{aligned}
$$
(Using R2→R2−R1 and R3→R3−R1 )
Taking out common factor (y−x) from R2 and (z−x) from R3, we get
$$
\Delta=(1+x y z)(y-x)(z-x)\left|\begin{array}{ccc}
1 & x & x^{2} \\
0 & 1 & y+x \\
0 & 1 & z+x
\end{array}\right|
$$
=(1+xyz)(y−x)(z−x)(z−y) (on expanding along C1)
Since Δ=0 and x,y,z are all different, i.e., x−y≠0,y−z≠0,z−x≠0, we get 1+ xyz=0
Related Playlists
Similar Questions
If x≠y≠zand∣∣ ∣ ∣∣xx21+x3yy21+y3zz21+z3∣∣ ∣ ∣∣=0, then the value of xyz is a.1 b. 2 c. −1 d. 2
View SolutionIf x, y, z are different and Δ=∣∣ ∣ ∣∣xx21+x3yy21+y3zz21+z3∣∣ ∣ ∣∣=0, then show that 1+xyz=0
View SolutionIf ∣∣ ∣ ∣∣xx21+x3yy21+y3zz21+z3∣∣ ∣ ∣∣=0 then relation of x,y and z is
View SolutionIf x,y,z are all distinct and
∣∣ ∣ ∣∣xx21+x3yy21+y3zz21+z3∣∣ ∣ ∣∣=0
then the value of xyz isView SolutionIf cos−1x+cos−1y+cos−1z=πandx+y+z=32, then prove that x=y=z
View SolutionIf ∣∣ ∣ ∣∣x3+1x2xy3+1y2yz3+1z2z∣∣ ∣ ∣∣=0 and x,y,z are all different then prove that xyz=−1
View SolutionIf x,y,z > 0 and x + y + z = 1, the prove that
2x1−x+2y1−y+2z1−z≥3.View SolutionIf ∣∣ ∣ ∣∣xx2x3+1yy2y3+1zz2z3+1∣∣ ∣ ∣∣ = 0 and x ,y and z are not equal to any other, prove that, xyz = -1
View SolutionIf ∣∣ ∣ ∣∣xx21+x3yy21+y2zz21+z3∣∣ ∣ ∣∣=0 and x,y,z are all distinct, then xyz is equal to
View SolutionIf ∣∣ ∣ ∣∣xx21+x3yy21+y2zz21+z3∣∣ ∣ ∣∣=0 and x,y,z are all distinct, then xyz is equal to
View Solution