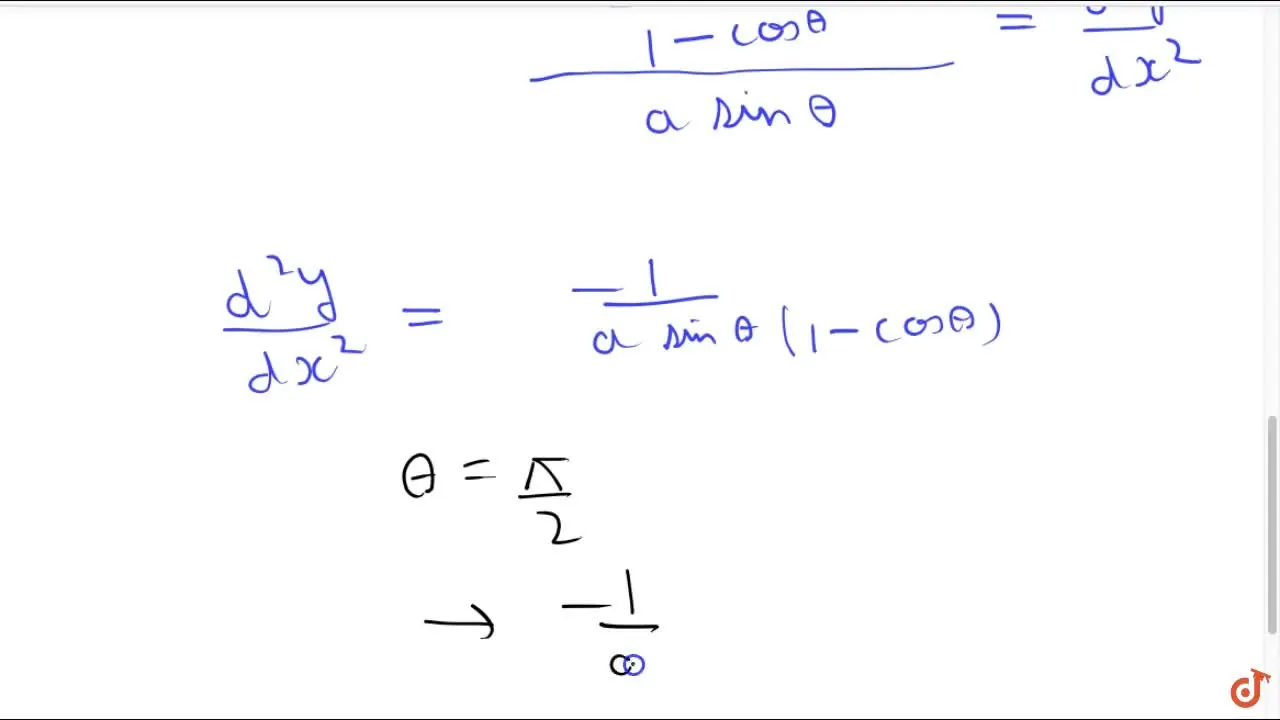If x=a(1−cosθ) , y=a(θ+sinθ) , prove that d2ydx2=−1a at θ=π2 .
Video Solution
Text Solution
Given asx=a(1−cosθ)...(1)
And
y=a(θ+sinθ)...(2)
On differentiating eqn (1) and (2) with respect to θ
dydθ=ddθa(θ+sinθ)=a(1+cosθ).......equation3
dxdθ=ddθa(1−cosθ)=asinθ.....equation4
{∵ddxcosx=−sinxddxsinx=cosx}
∴dydx=dydθdxdθ=a(1+cosθ)asinθ=(1+cosθ)sinθ.....equation5
Again, on differentiating with respect to x
&ddx(dydx)=ddx((1+cosθ)sinθ)=ddx(1+cosθ){cosec}θ
&d2ydx2={{cosec}θddθ(1+cosθ)+(1+cosθ)ddθ{cosec}θ}dθdx
&d2yd2={{cosec}θ(−sinθ)+(1+cosθ)(−{cosec}θcotθ)}1asinθ
&d2ydx2={−1−{cosec}θcotθ−cot2θ}1asinθ
&d2yd2=−1aatθ=π2
∴putθ=π2 in above equation
{d}2{y}{dx}2={−1−{cosec}π2cotπ2−cot2π2}1{asin}π2
={−1−0−0}1a
d2ydx2=−1a
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If x=a(1−cosθ) , y=a(θ+sinθ) , prove that d2ydx2=−1a at θ=π2 .
View SolutionIf x=a(1+cosθ) , y=a(θ+sinθ) , prove that d2ydx2=−1a at θ=π2 .
View SolutionIf x=a(1−cos3θ) , y=a s∈3θ , prove that d2ydx2=3227 a at θ=π6 .
View SolutionIf x=a(θ+sinθ) , y=a(1+cosθ) , prove that d2ydx2=−ay2 .
View SolutionIf x=cosθ(1+cosθ),y=sinθ(1+cosθ), then (dydx) at θ=π2 is
View SolutionIf y=a(θ+sinθ),x=a(1−cosθ), then dydx=
View SolutionIf x=θ−1θ and y=θ+1θ, then: d2ydx2=
View SolutionIf x=θ−sinθ,y=1−cosθ,thend2ydx2=
View SolutionIf x=sinθ,y=sin3θ then d2ydx2 at θ=π2 is . . .
View SolutionIf x=a(θ+sinθ),y=a(1+cosθ),y=a(1+cosθ), Prove that d2ydx2=−ay2
View Solution