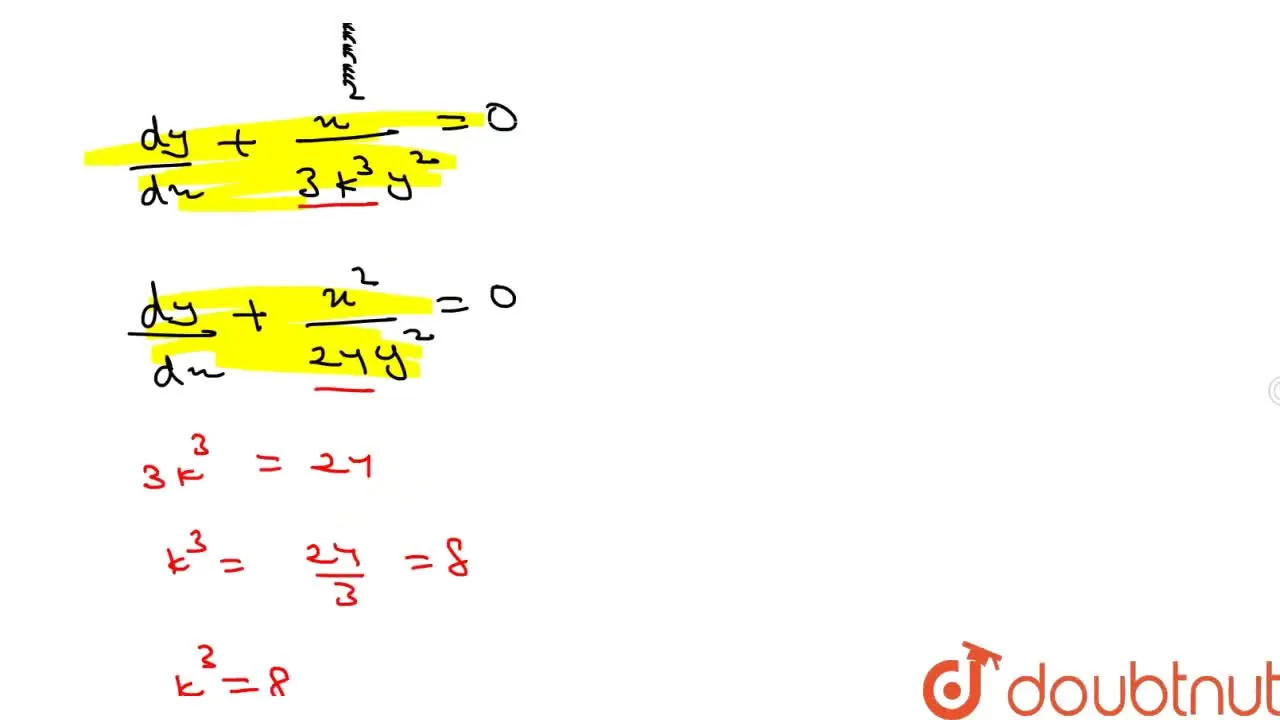
If x3+3(ky)3=k3 and dydx+x224y2=0, then k is (where k > 0)
32
2
23
3
The correct Answer is:B
Differentiating both sides
x3+3(ky)3=k3, 3x2+9k3y2dydx=0
dydx=−x23k3y2
On comparing with given equation −13k3=−124, k3=8⇒k=2
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 24 EXERCISE - MATHEMATICS (SECTION - 2)5videos
JEE MAIN REVISION TEST- 24
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 16EXERCISE - MATHEMATICS (SECTION 2)5videos
JEE MAIN REVISION TEST- 16
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE Main Revision Test-20 | JEE-2020 EXERCISE - MATHEMATICS25videos
JEE Main Revision Test-20 | JEE-2020
Similar Questions
If d2xdy2(dydx)3+d2ydx2=k , then k is equal to
View SolutionLet xk+yk=ak,(a,k>0) and dydx+(yx)5/3=0 , then k=
View SolutionIf y=sin(8sin−1x) then (1−x2)d2ydx2−xdydx=−ky, where k =
View SolutionIn the line 3x−y=k is a tangent to the hyperbola 3x2−y2=3,then k =
View SolutionIf d2xdy2(dydx)3+d2ydx2=Kthen the value of k is equal to
View SolutionThe value of sin−1{(sin.π3)x√(x2+k2−kx)}−cos_1{(cos.π6)x√(x2+k2−kx)} , where(k2<x<2k,k>0) is
View SolutionIf the solution of the differential equation y3x2cos(x3)dx+sin(x3)y2dy=x3dx is 2sin(x3)yk=x2+C (where C is an arbitrary constant), then the value of k is equal to
View SolutionIf the independent variable x is changed to y, then the differential equation xd2ydx2+(dydx)3−dydx=0 is changed to xd2xdy2+(dxdy)2=k where k equals____
View SolutionIf the independent variable x is changed to y, then the differential equation xd2ydx2+(dydx)3−dydx=0 is changed to xd2xdy2+(dxdy)2=k where k equals____
View SolutionIf the area bounded by y=2−|2−x|andy=3|x| is k−3ln32, then k is equal to _____.
View Solution