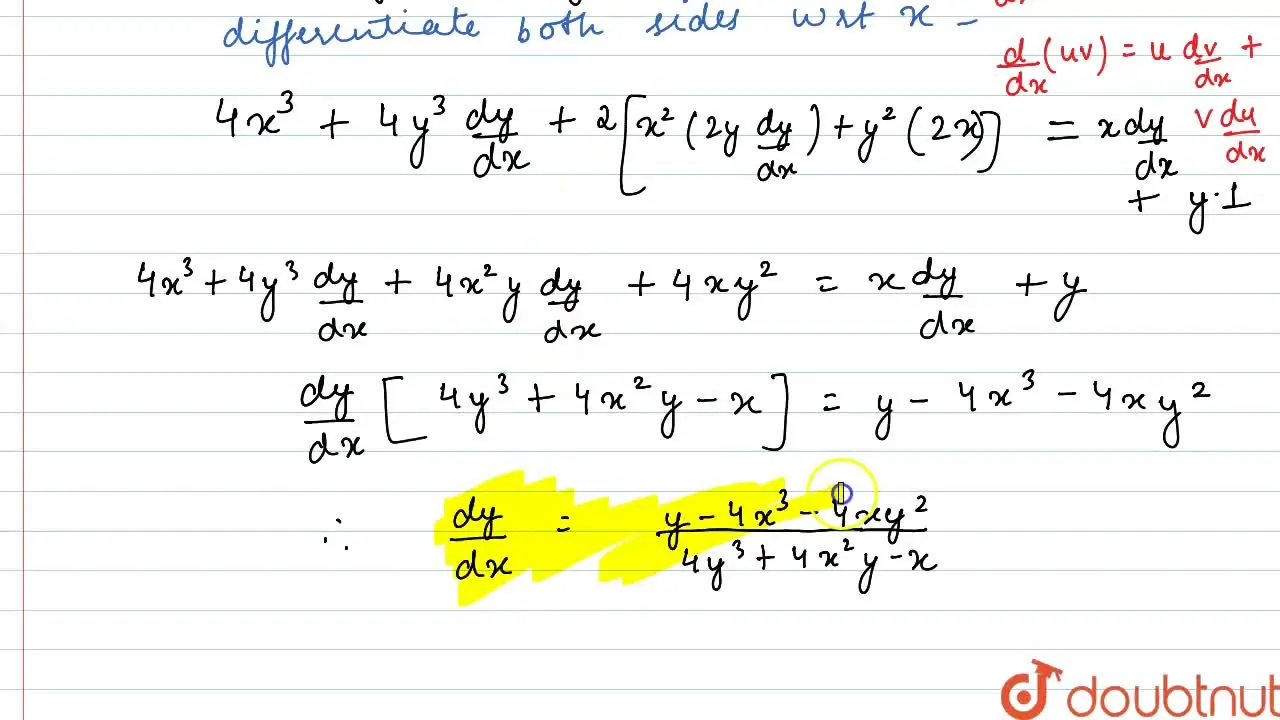If (x2+y2)2=xy , find dydx
Video Solution
Text Solution
The correct Answer is:N/a
We have, (x2+y2)2=xy
On differentiating both sides w.r.t. x, we get
ddx(x2+y2)2=ddx(xy)
⇒2(x2+y2).ddx(x2+y2)=x.ddx+y.ddxx
⇒2(x2+y2).(2x+2y'dydx)=x'dydx+y
⇒2x2.2x+2x2.2y'dydx+2y2.2x+2y2.2y'dydx=x'dydx+y
⇒dydx[4x2y+44y3−x]=y−4x3−4xy2
∴dydx=(y−4x3−4xy2)(4x2y+4y3−x)
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Objective type28videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Fillers10videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions22videos
APPLICATION OF INTEGRALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DETERMINANTSEXERCISE - TRUE/FALSE11videos
DETERMINANTS
Similar Questions
If (x+y)2=2axy , find dydx
View SolutionIf xy=c2 , find dydx
View SolutionIf sin(xy)+yx=x2−y2 , find dydx .
View SolutionIf xy+y2=tanx+y ,then find dydx
View SolutionIf y3−3xy2=x3+3x2 y , find dydx
View SolutionIf xy+yx=2, find dydx .
View SolutionIf y2=ax2+bx+c , then find (dy)/(dx)
View SolutionIf y=cos2x, then find dydx.
View Solutiony2+x2dydx=xydydx
View SolutionIf xy=2x−y then Find dydx=
View Solution