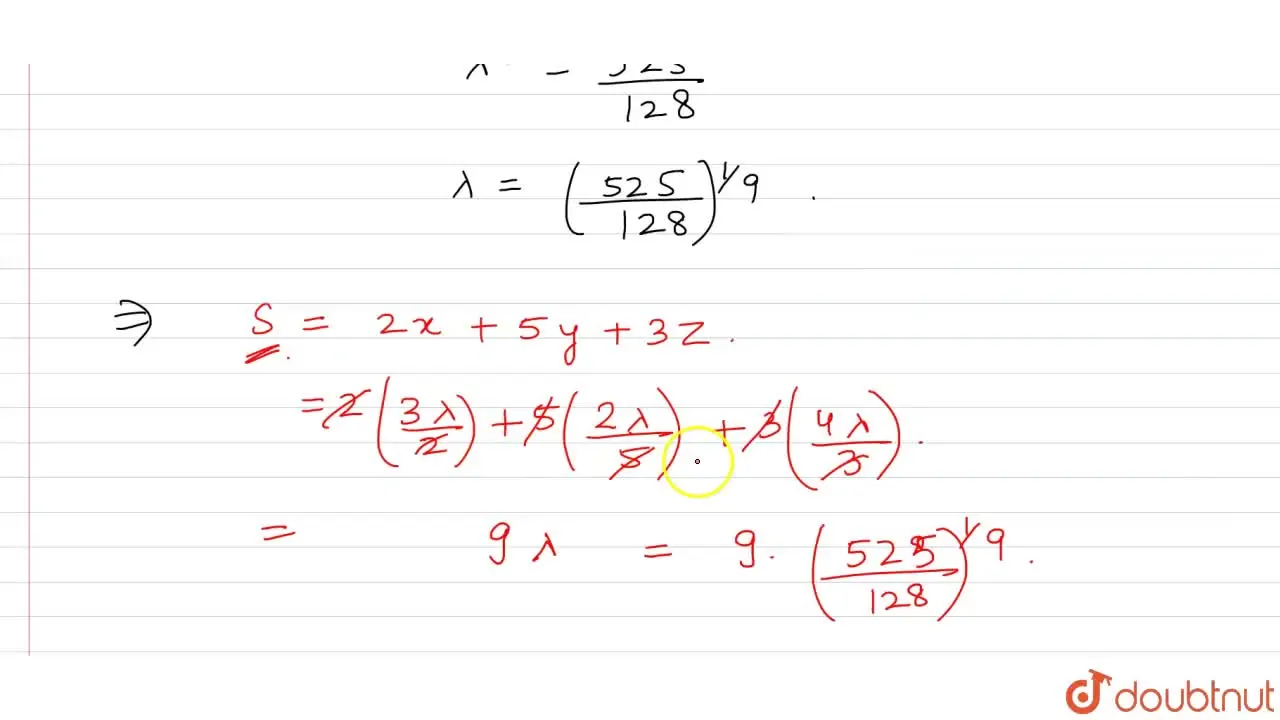If x, y, z are positive real numbers such that x3y2z4=7, then the least value of 2x+5y+3z, is
(525128)1/9
3(525128)1/9
9(525128)1/9
none of these
The correct Answer is:C
Let S=2x5y+3z.
Since x3y2z4=7 is the product of 9 terms viz. 3x's,2y's and 4z's. So we write S as the sum of 9 terms as given below.
S=3(2x3)+2(5y2)+4(3z4)
Now,
P=(2x3)3(5y2)2(3z4)4
⇒ P=(23)3(52)2(34)4(x3y2z4)
⇒ P=(23)3(52)2(34)4×7 [∵x3y2z4=7(given)]
⇒ P=525128, a constant.
Therefore, S is least when
2x3=5y2=3z4=λ(say)
⇒ x=3λ2,y=2λ5 and z=4λ3
∴ x3y2z4=7
⇒ (32)3(25)2(43)4λ9=7⇒λ9=(525128)⇒λ=(525128)1/9
Thus, the least value of S is given by
S=2×3λ2+5(2λ5)+3(4λ3)=9λ=9(525128)1/9
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section 2 - Assertion Reason Type9videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section I - Mcqs37videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - INEQUALITIES EXERCISE - Section II - Assertion Reason Type1videos
INEQUALITIES
- BOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Chapter Test29videos
HYPERBOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
Similar Questions
If x, y, z are positive real numbers such that x+y+z=a,then
View SolutionIf x,y,z are positive real numbers such that x2+y2+Z2=7 and xy+yz+xz=4 then the minimum value of xy is
View SolutionIf x.y,z are positive real numbers such that x2+y2+z2=27, then x3+y3+z3 has
View SolutionIf x, y, z are real numbers such that x+y+z=4 and x2+y2+z2=6, then x,y,z lie in :
View SolutionIf a,y and z are real numbers such that x2+y2+2z2=4x−2z+2yz−5, then the possible value of (x-y-z) is :
View SolutionIf x,y andz are three real numbers such that x+y+z=4 and x2+y2+z2=6,then show that each of x,y and z lie in the closed interval [23,2]
View SolutionThe x,y,z are positive real numbers such that (log)2xz=3,(log)5yz=6,and(log)xyz=23, then the value of (12z) is ............
View SolutionLet x,y,z be positive real numbers such thatlog2xz=3,log5yz=6 and logxyz=23 then the value of z is
View SolutionIf x,y,z are positive real numbers such that y,z,x are in G.P. and x+y+z=xyz then the maximum value of equals 76x4+x2+7 equals
View SolutionIf x, y, z are real numbers such that x+y+z=4 and x2+y2+z2=6, then x,y,z lie in :
View Solution