If x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=sin3t√cos2t,y=cos3t√cos2t
y=cos3t√cos2t
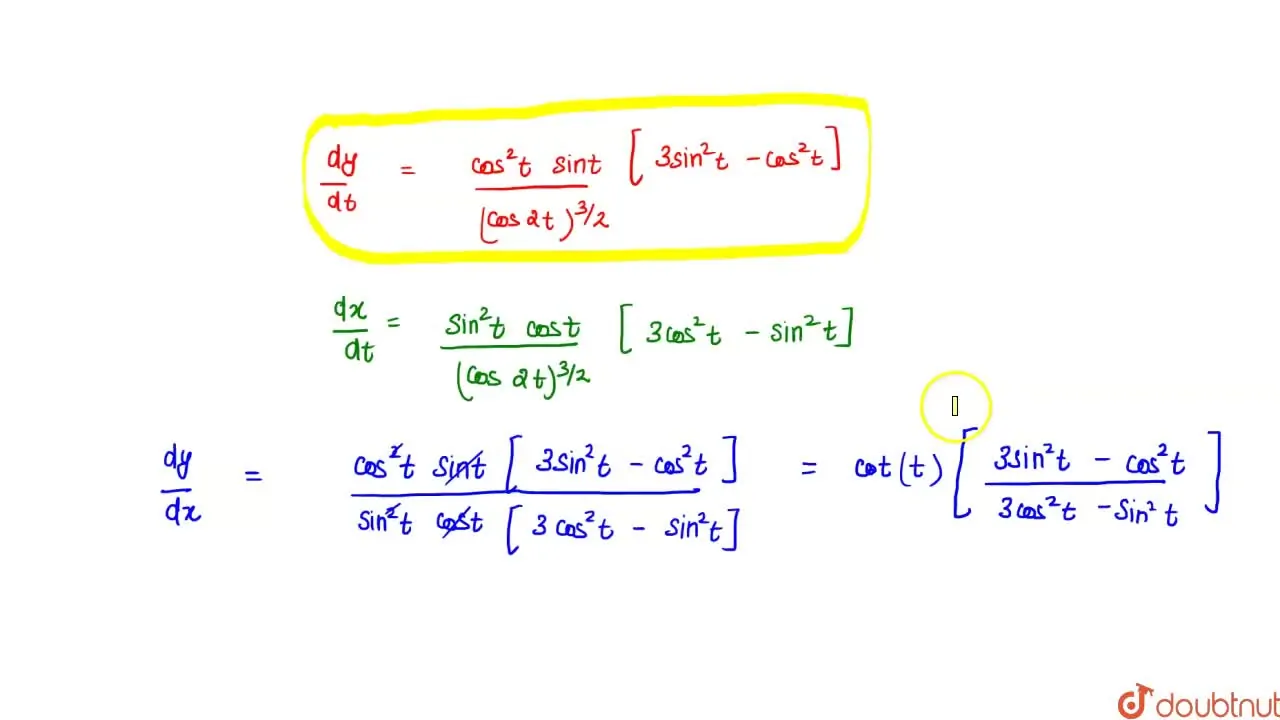
dydt=1cos2t(√cos2t(3cos2t)(−sint)−cos3t(12(1√cos2t(−sin2t)(2)))
dydt=1cos2t(−√cos2t(3cos2t)(sint)+cos3tsin2t√cos2t)
dydt=1(cos2t)(√cos2t)(cos3tsin2t−3cos2tsintcos2t)→(1)
x=sin3t√cos2t
dxdt=1cos2t(√cos2t(3sin2t)(cost)−sin3t(12(1√cos2t(−sin2t)(2)))
dxdt=1cos2t(√cos2t(3sin2t)(cost)+sin3tsin2t√cos2t)
dxdt=1(cos2t)(√cos2t)(3sin2tcostcos2t+sin3tsin2t)→(2)
Dividing (1) by (2),
dydx=cos3tsin2t−3cos2tsintcos2t3sin2tcostcos2t+sin3tsin2t
Similar Questions
If x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=sin3t√cos2t,y=cos3t√cos2tView SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=sint,y=cos2tView SolutionFind dydx , if x=sin3t√cos2t , y=cos3t√cos2t
View SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=4t,y=4tView SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=2at2,y=at4View SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=a(cost+logtan(t2)),y=asintView SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=acosθ,y=bcosθView SolutionIf x and y are connected parametrically by the equations given in, without eliminating the parameter, find dydx.
x=asect,y=btant.View SolutionIf x and y are connected parametrically by the equations given in, without eliminating the parameter, find dydx.
x=t2−2t,y=t4−4tView SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=a(θ−sinθ),y=a(1+cosθ)View Solution