If →a,→b,→cand→d are the position vectors of the vertices of a cycle quadrilateral ABCD, prove that ∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d+→d×→b∣∣(→b−→c).(→d−→c)
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)=∣∣(→a−→d)×(→b−→a)∣∣(→b−→a).(→d−→a)
=∣∣→a−→d∣∣∣∣→b−→a∣∣sinA∣∣→b−→a∣∣∣∣→d−→a∣∣cosA
tanA
Also∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=∣∣(→b−→c)×(→c−→d)∣∣(→b−→a).(→d−→c)
=∣∣→b−→c∣∣∣∣→c−→d∣∣sinC∣∣→b−→c∣∣.∣∣→d−→c∣∣cosA
tanC
As it is a cycle quadrilateral, we have
A=180∘−C
tanA=tan(180∘−C)
tanA+tanC=0
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)

Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise337videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DETERMINANTSEXERCISE - Question Bank23videos
DETERMINANTS
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank25videos
DIFFERENTIAL EQUATIONS
Similar Questions
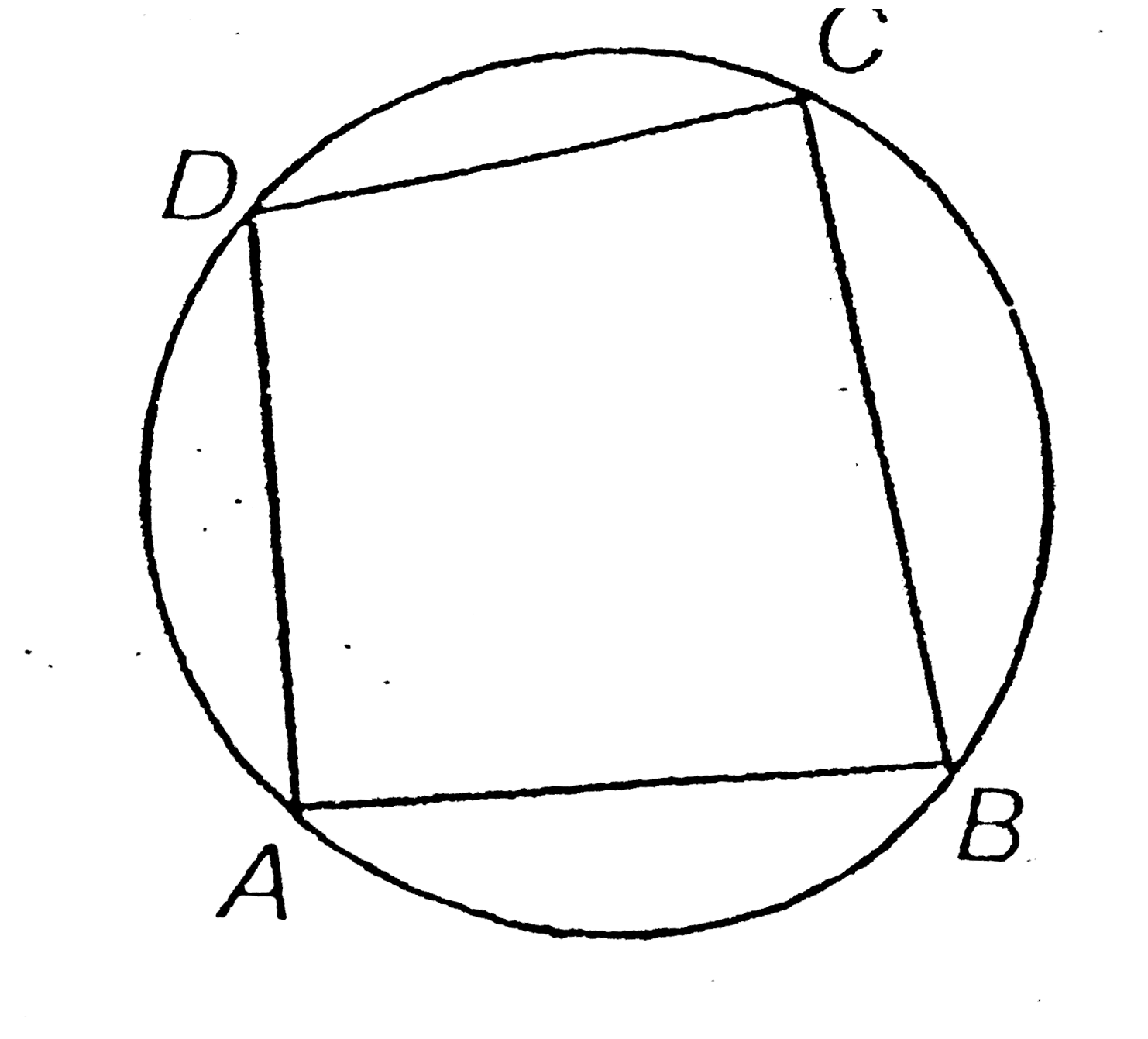
If →a,→b,→c,→d are the position vectors of the verticles of a cyclic quadrilateral ABCd prove that
∣∣→a×→b+→b×→d+→d×→a∣∣(→b−→a).(→d−→a)+∣∣→b×→c+→c×→d+→d×→b∣∣(→b−→c).(→d−→c)=0
 View Solution
View SolutionProve that: [(→a×→b)×(→a×→c)].→d=[→a→b→c](→a.→d)
View SolutionProve that: (→a×→b)×(→c×→d)+(→a×→c)×(→d×→b)+(→a×→d)×(→b×→c)=2[→b→c→d]→a
View SolutionProve that →a×{→b×(→c×→d)}=(→b.→d)(→a×→c)−(→b.→c)(→a×→d)
View SolutionProve that →a'×→b'+→b'×→c'+→c'×→a'=→a+→b+→c[→a→b→c]
View SolutionIf →a,→b,→cand→d ar distinct vectors such that →a×→c=→b×→dand→a×→b=→c×→d. Prove that (→a−→d).(→c−→b)≠0,i.e.,→a.→b+→d.→c≠→d.→b+→a.→c.
View SolutionShow that: (→a−→d)×(→b−→c)+(→b−→d)×(→c−→a)+(→c−→d)×(→a−→b) is independent of →d.
View SolutionIf →a,→b,→c,→d are coplanar vectors, then (→a×→b)×(→c×→d)=
View SolutionIf [→a→b→c]=1 then value of →a.→b×→c→c×→a.→b+→b.→c×→a→a×→b.→c+→c.→a×→b→b×→c.→a is
View SolutionProve that [→a→b+→c→d]=[→a→b→d]+[→a→c→d]
View Solution


