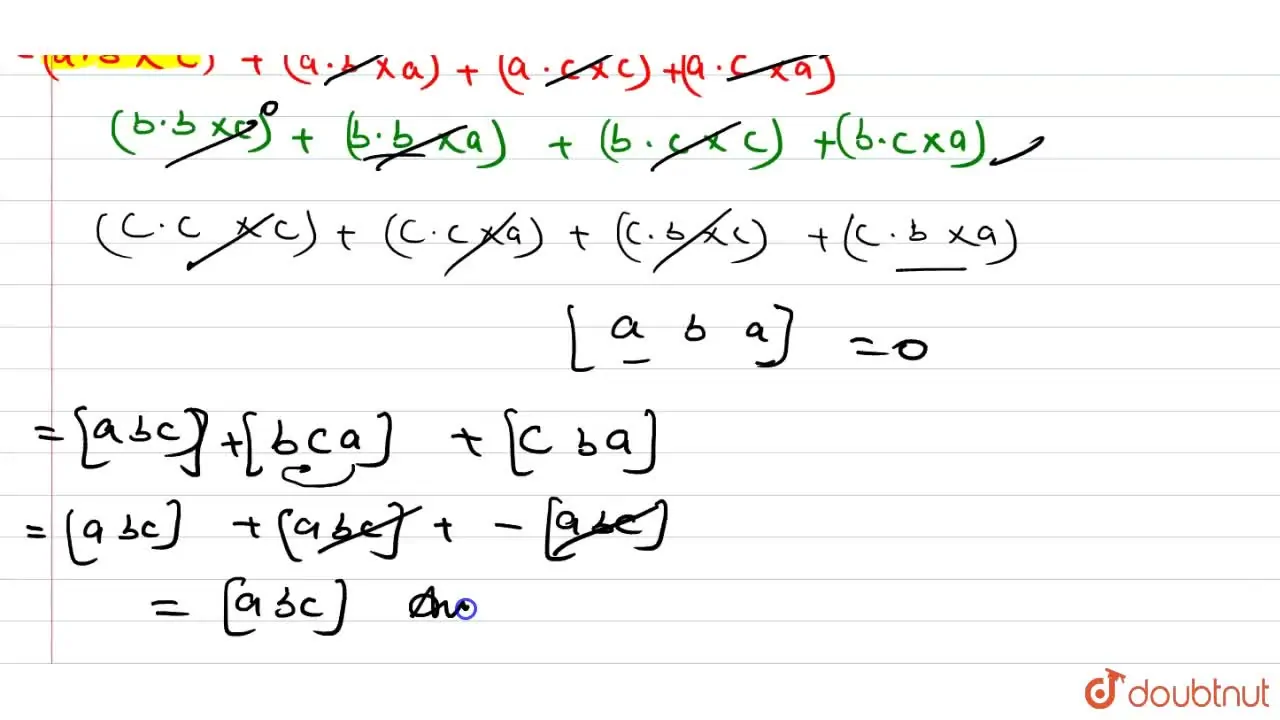If →a,→b,→c are any three non coplanar vectors, then
(→a+→b+→c).(→b+→c)×(→c+→a)
0
[→a→b→c]
2[→a→b→c]
3[→a→b→c]
The correct Answer is:B
We have
(→a+→b+→c).(→b+→c)×(→c+→a)
=[→a+→b+→c→b+→c→c+→a]=∣∣
∣∣111011101∣∣
∣∣[→a→b→c]=[→a→b→c]
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Section II - Assertion Reason Type12videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test60videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALER AND VECTOR PRODUCTS OF TWO VECTORS EXERCISE - Section I - Solved Mcqs12videos
SCALER AND VECTOR PRODUCTS OF TWO VECTORS
Similar Questions
If →a,→b,→c are any three non coplanar vectors, then [→a+→b+→c→a−→c→a−→b] is equal to
View SolutionIf →a,→band→c1 are three non-coplanar vectors, then (→a+→b+→c).[(→a+→b)×(→a+→c)] equals
View SolutionIf →a,→band→c1 are three non-coplanar vectors, then (→a+→b+→c).[(→a+→b)×(→a+→c)] equals
View SolutionIf →a,→b,→c are non-coplanar vectors, then →a.(→b×→c)→b.(→c×→a)+→b.(→c×→a)→c.(→a×→b)+→c.(→b×→a)→a.(→b×→c) is equal to:
View SolutionIf →a,→b,→c are three non coplanar, non zero vectors then (→a.→a)(→b×→c)+(→a.→b)(→c×→a)+(→a.→c)(→a×→b) is equal to
View SolutionIf →a,→b,→c are three on-coplanar vectors such that →a×→b=→c,→b×→c=→a,→c×→a=→b, then the value of |→a|+∣∣→b∣∣+|→c| is
View SolutionIf →a,→b,→c are non-null non coplanar vectors, then
[→a−2→b+→c→b−2→c+→a→c−2→a+→b]=View SolutionIf →a,→b,→c are non-coplanar vectors, then →a.(→b×→c)(→c×→a).→b+→b.(→a×→c)→c.(→a×→b) is equal to
View SolutionIf →a,→b,→c are non-coplanar vectors, then →a.(→b×→c)(→c×→a).→b+→b.(→a×→c)→a.(→a×→b) is equal to
View SolutionIf →a,→band→c are three non-coplanar non-zero vectors, then prove that (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b=[→b→c→a]→a
View Solution