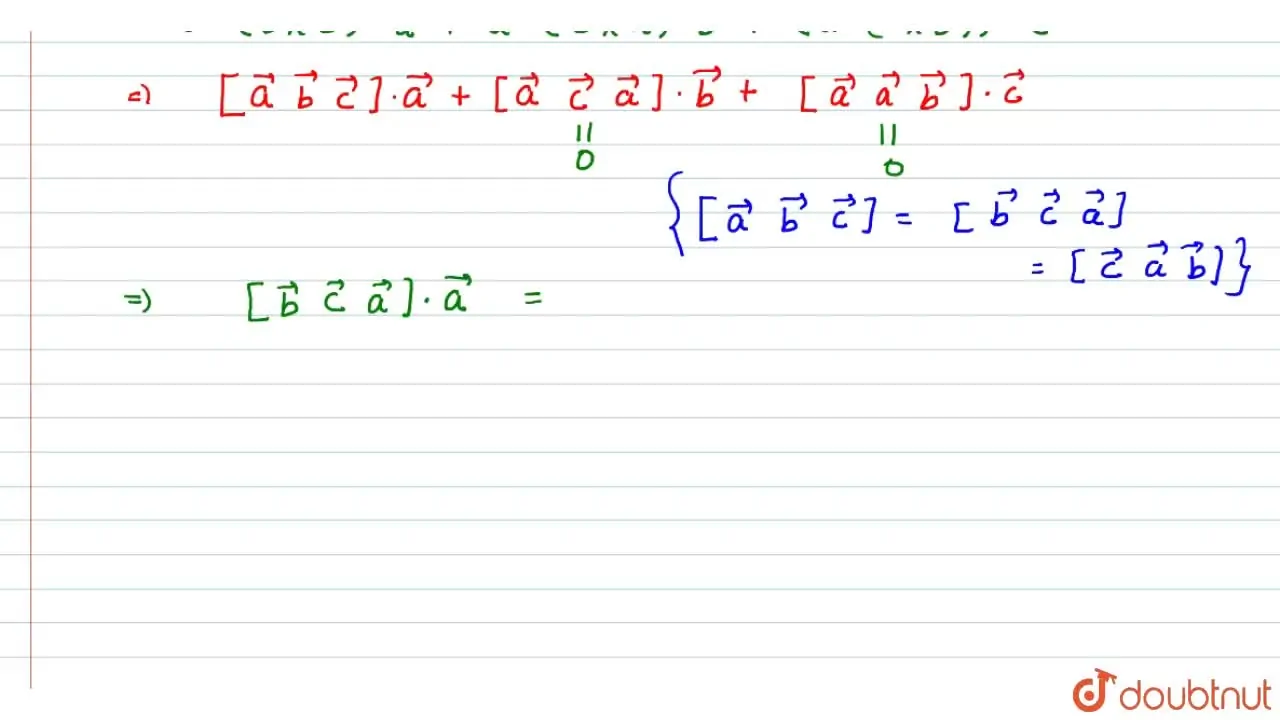If →a,→band→c are three non-coplanar non-zero vectors, then prove that (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b=[→b→c→a]→a
As →a,→band→c are non- coplanar, →b×→a,→c×→aand→a×→b are also non-coplanar, So, any vector con be expressend as a linear combination of these vectors.
→a=λ→b×→c+μ→c×→a+v→a×→b
→a.→a=λ[→b→c→a],→a.→b=μ[→c→a→b],→a.→c=v[→a→b→c]
→a=(→a.→a)→b×→c[→b→c→a]+(→a.→b)→c×→a[→c→a→b]+(→a.→c)→a×→b[→a→b→c]
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.118videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.215videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions264videos
DETERMINANTS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type5videos
DIFFERENTIAL EQUATIONS
Similar Questions
If →a,→b,→c are three non coplanar, non zero vectors then (→a.→a)(→b×→c)+(→a.→b)(→c×→a)+(→a.→c)(→a×→b) is equal to
View SolutionIf →a,→band→c are three non-zero non-coplanar vectors, then the value of (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b.
View SolutionIf a,bandc are three non-cop0lanar vector, non-zero vectors then the value of (→a.→a)→b×→c+(→a.→b)→c×→a+(→a.→c)→a×→b.
View SolutionIf →a,→band→c are three non-coplanar vectors, then (→a+→b+→c).[(→a+→b)×(→a+→c)] equals
View SolutionIf →a,→b,→c are any three non coplanar vectors, then
(→a+→b+→c).(→b+→c)×(→c+→a)View SolutionIf →a,→b,→c are non-coplanar vectors, then →a.(→b×→c)→b.(→c×→a)+→b.(→c×→a)→c.(→a×→b)+→c.(→b×→a)→a.(→b×→c) is equal to:
View Solutioni. If →a,→band→c are non-coplanar vectors, prove that vectors 3→a−7→b−4→c,3→a−2→b+→cand→a+→b+2→c are coplanar.
View SolutionIf →a,→b,→c are three non-zero vectors such that →a+→b+→c=0 and m=→a.→b+→b.→c+→c.→a, then:
View Solution→a,→band→c are three non-coplanar vectors and →r. Is any arbitrary vector. Prove that [→b→c→r]→a+[→c→a→r]→b+[→a→b→r]→c=[→a→b→c]→r.
View SolutionFor any four vectors, prove that (→a×→b)×(→c×→d)=[→a→c→d]→b−[→b→c→d]→a
View Solution