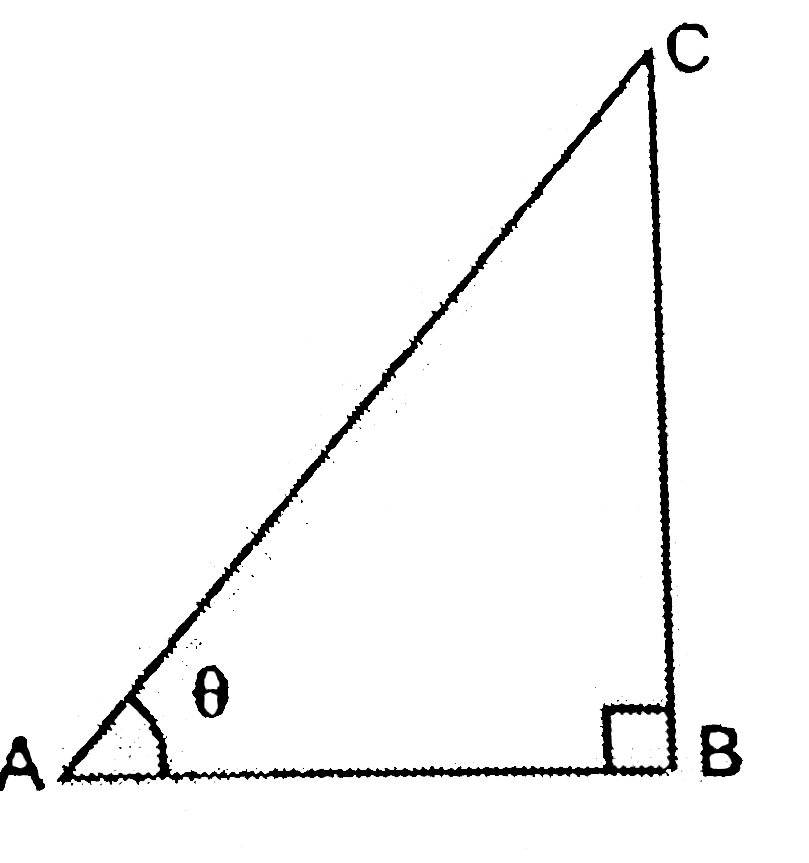
If the sum of a side and hypotenuse of a right angled triangle is given then show that area of triangle will be maximum when the angle between side and the hypotenuse is π/3.
Let, In ΔABC,∠B=90∘
Let AB = x and AC = y
Then x+y = k
Which is given a constant.
BC=√AC2−AB2
=√y2−x2
=√(k−x)2−x2
=√k2−2kx
Now area of ΔABC
Δ=12×AB×BC
=12×x×√k2−2kx
⇒Δ2=14x2(k2−2kx)
LetΔ2=S,
∴S=14k(kx2−2x3)
⇒dSdx=14k(2kx−6x2)
For maxima/minima
dSdx=0
⇒2kx−6x2=0
⇒x=k3
and d2Sdx2=14k(2k−12x)
at x=k3
d2Sdx2=14k(2k−4k)=−k22<0
∴ At x=k3,⋅S is maximum
⇒ At x=k3,Δ2 is maximum
⇒ At x=k3,Δ is maximum
and y=k−k3=2k3
If ∠BAC=θ, then
cosθ=ABAC=xy=k/32k/3=12
⇒θ=π/3 π/3 for maximum area.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6a20videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6b11videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
Similar Questions
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π3.
View SolutionIf the sum of the lengths of the hypotenues and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is π/3 .
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionThe hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
View SolutionIf the length of the hypotenuse of a right angled triangle is 10 cm, then what is the maximum area of such a right angled triangle?
View SolutionA side of an isosceles right angled triangle is x. Find its hypotenuse.
View SolutionThe sum of the cubes of the legs of a right angled triangle is less than the cube of the hypotenuse.
View SolutionFind the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View Solution


