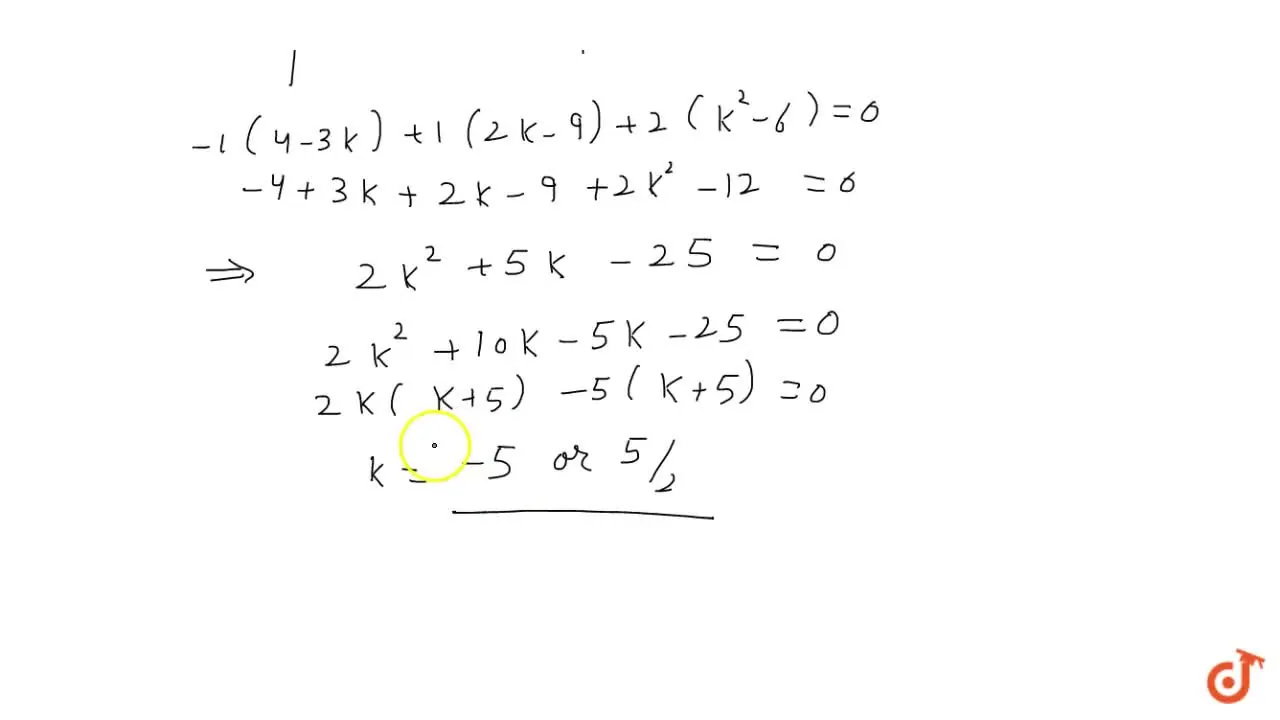If straight lines x−1k=y−22=z−33 and x−23=y−3k=z−12 intersect at a point, then the integer value of |k| is equal to (1) −5 (2) 5 (3) 2 (4) −2
L1=x−1k=y−22=z−33
L2=x−23=y−3k=z−12
L1&L2 are in same plane
L1 passes from (1,2,3) and L2 passes from (2,3,1)
Dr's=(−1,−1,2)
Dr's of line L1=(k,2,3)
Dr's of line L2=(3,k,2)
∴ plane
∣∣
∣∣−1−12k233k2∣∣
∣∣=0
−1(4−3k)+1(2k−9)+2(k2−6)=0
−4+3k+2k−9+2k2−12=0
2k2+5k−25=0
k=−5or52
option 1 is correct
Related Playlists
Similar Questions
If the straight lines x−1k=y−22=z−33andx−23=y−3k=z−12 intersect at a point, then the integer k is equal to
View SolutionIf the straight lines x−1k=y−22=z+33 and x−23=y−3k=z−13 intersect at a point ,then the integer k is equal to
View SolutionIf the straight lines
x−1k=y−22=z−33 and x−23=y−3k=z−12 intersect at a point, then integer k is equal toView SolutionIf the straight lines x−1k=y−22=(z−3)andx−23=y−3k=(z−1) intersect at a point, then the integer k is equal to
View SolutionIf straight lines x−1k=y−22=z−33 and x−23=y−3k=z−12 intersect at a point, then the integer value of |k| is equal to (1) −5 (2) 5 (3) 2 (4) −2
View SolutionTwo lines x−12=y+13=z−14 and x−31=y−k2=z intersect at a point A and B.
View SolutionIf the lines x−12=y+13=z−14andx−31=y−k2=z1 intersect then the value of k is (A) 29 (B) 92 (C) 0 (D) -1
View SolutionIf the two lines x−13=y−k6=z+1−2andx−2−1=y−24=z+1−1 intersect at a point, then k is
View SolutionIf the lines x−11=y−31=z−2λ and x−1λ=y−32=z−41 intersect at a point, then the value of λ2+4 is equal to
View SolutionIf the straight lines
x−1k=y−22=z−33 and x−23=y−3k=z−12 intersect at a point, then integer k is equal toView Solution