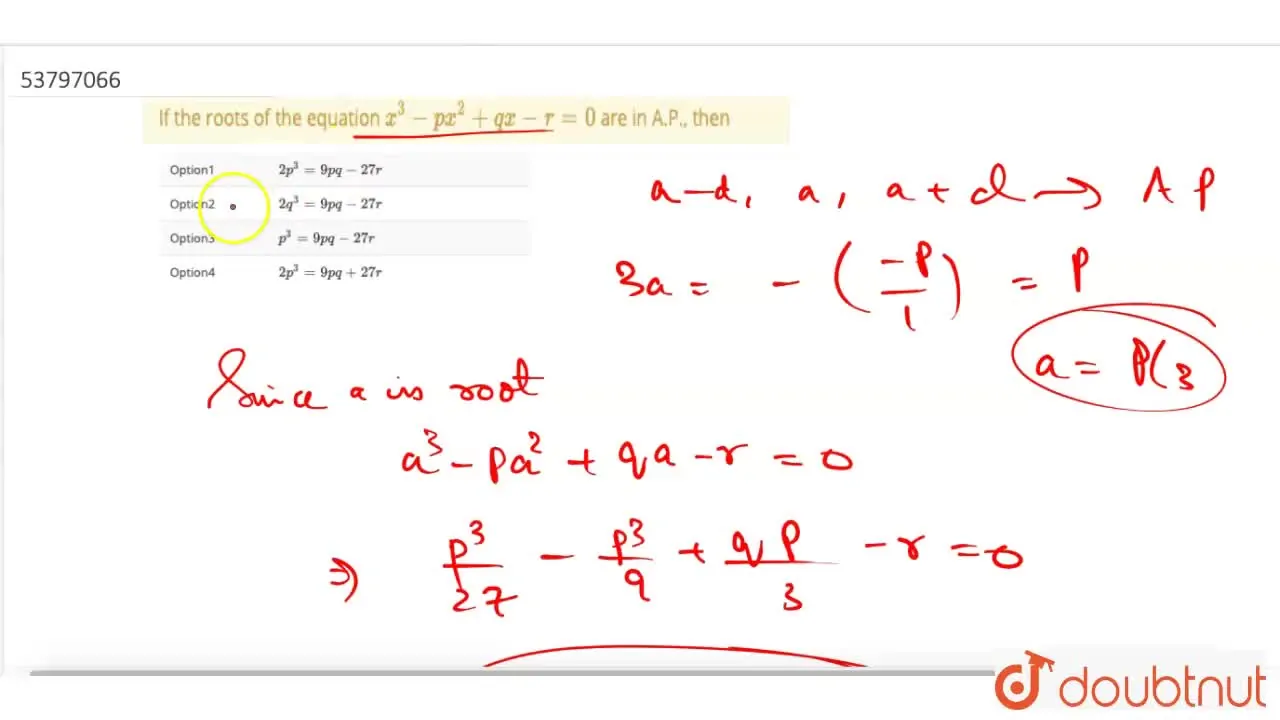
If the roots of the equation x3−px2+qx−r=0 are in A.P., then
2p3=9pq−27r
2q3=9pq−27r
p3=9pq−27r
2p3=9pq+27r
The correct Answer is:A
Let the roots of the given equation be a - d, a, a + d. Then,
(a−d)+a+(a+d)=−−p1⇒a=p3
Since a is a root of the given equation.
∴ a3−pa2+qa−r=0
⇒ p327−p39+qp3−r=0⇒2p3−9pq+27r=0
This is the required condition.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Section I - Solved Mcqs123videos
QUADRATIC EXPRESSIONS AND EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Section II - Assertion Reason Type22videos
QUADRATIC EXPRESSIONS AND EQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test60videos
SEQUENCES AND SERIES
Similar Questions
If two roots of x3−ax2+bx−c=0 are equal in magnitude but opposite in sign. Then:
View SolutionIf 2p3−9pq+27r=0 then prove that the roots of the equations rx3−qx2+px−1=0 are in Н.Р.
View SolutionFind the conditions if roots of the equation x3−px2+qx−r=0 are in
(i) AP (ii)GP
(iii) HPView SolutionIf the roots of the equation, x3+px2+qx−1=0 form an increasingG.P. wherep and qare real,then
View SolutionIf two roots of the equation x3−px2+qx−r=0 are equal in magnitude but opposite in sign, then:
View SolutionIf the roots of the equation x3+3px2+3qx−8=0 are in a Geometric progression then q3p3=
View SolutionIf sin α and cos α are the roots of the equation px2 +qx+r = 0,then
View SolutionIf the roots of the equation px2+qx+r=0 are in the ratio l:m then
View SolutionIf the roots of the equation px2+qx+r=0, where 2p,q,2r are in G.P, are of the form α2,4α−4. Then the value of 2p+4q+7r is :
View SolutionIf sinα and cosα are the roots of the equation px2+qx+r=0, then
View Solution