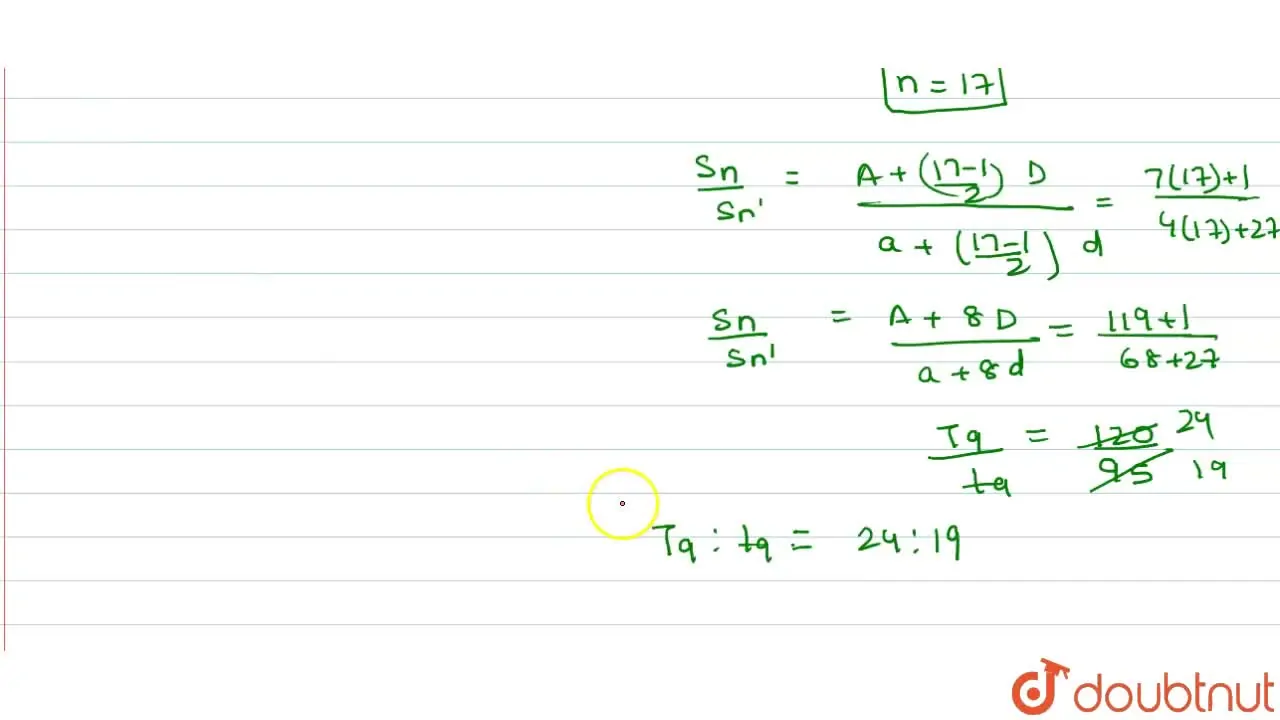If the ratio of the sum of the first n terms of two Aps is (7n + 1) : (4n + 27) then find the ratio of their 9th terms.
Let a1anda2 be the first terms and d1andd2 be the common difference of the two Aps respectively.
Let SnandS'n be the sum of the first n terms of the two Aps and TnandT'n be their nth terms respectively.
Then, SnS'n=7n+14n+27⇒n2[2a1+(n−1)d1]n2[2a2+(n−1)d2]=7n+14n+27
2a1+(n−1)d12a2+(n−1)d2=7n+14n+27. ...(i)
To find the ratio of mth terms, we replace n by (2m-1) in the above expression.
Replacing n by (2×9−1), i.e., 17 on both sides in (i), we get
2a1+(17−1)d12a2+(17−1)d2=7×17+14×17+27⇒2a1+16d12a2+16d2=12095
⇒a1+8d1a2+8d2=2419
⇒a1+(9−1)d1a2+(9−1)d2=2419
⇒TnT'n=2419
∴ required ratio = 24 : 19.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 5A48videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 5B13videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Test Yourself19videos
AREA OF CIRCLE, SECTOR AND SEGMENT
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself20videos
CIRCLES
Similar Questions
The ratio of sums of n terms of two A.P'. is (7n + 1) : (4n + 27). Find the ratio of their 11th terms.
View SolutionThe ratio of the sum of n terms of two A.Ps is (7n+1):(4n+27). Find the ratio of their mth terms.
View SolutionThe ratio of the sum of n terms of two A.P. s is (7n+1):(4n+27) . Find the ratio of their mth terms.
View SolutionIf the ratio of the sum of n terms of two AP's be (7n+1):(4n+27), then the ratio of their 11th terms will be
View SolutionThe ratio of the sum of n terms of two A.P.'s is (7n−1):(3n+11), find the ratio of their 10th terms.
View SolutionIf the ratio of the sum of 'n' terms of two A.P's is (5n+4) : (9n+6), find the ratio of the 18th terms of these A.P.'s.
View SolutionIf the sums of n terms of two Aps are in the ratio ( 2n+3) :(3n+2) , find the ratio of their 10th terms.
View SolutionThe sums of first n terms of two A.P. 's are in hte ratio (7n+2):(n+4). Find the ratio of their 5th terms.
View SolutionThe ratio of the sum of n terms of two A.P.'s is (3n+1):(4n+3). Find the ratio of their mth terms.
View SolutionIf the ratio of sum to n terms of two A.P's is (5n+7): (3n+2), then the ratio of their 17th terms is
View Solution