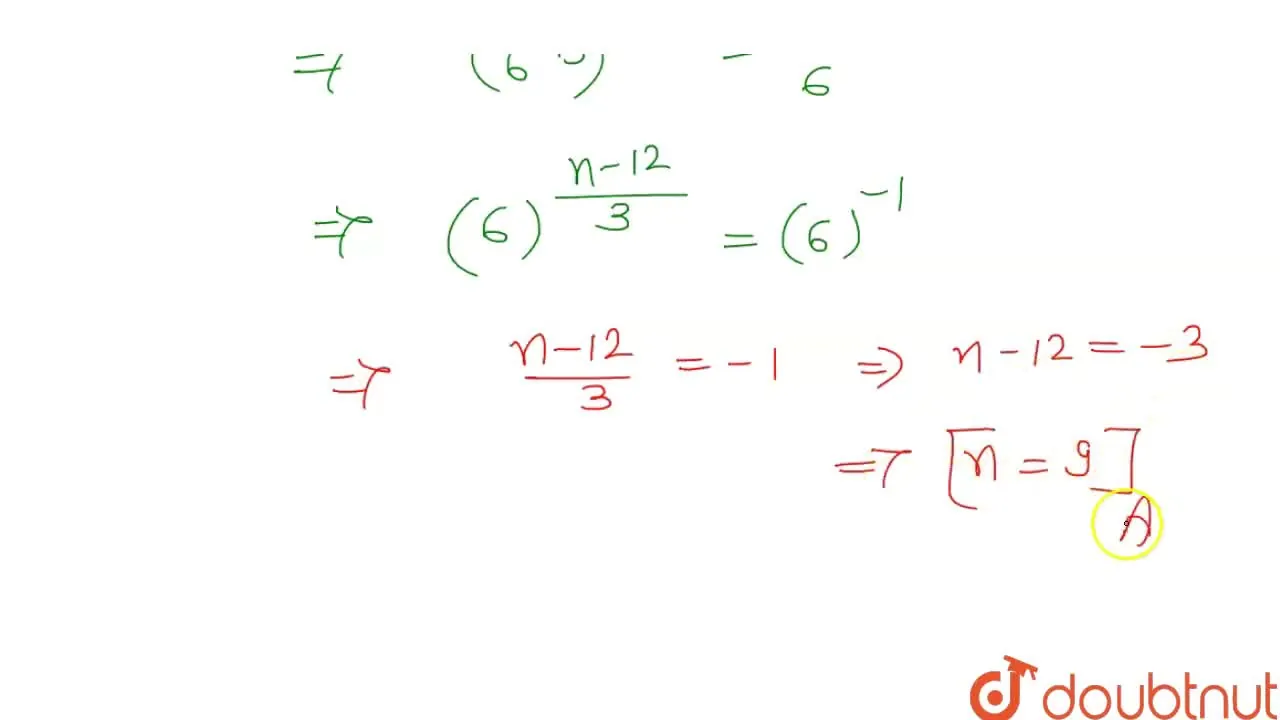If the ratio of 7th term from the beginning to the seventh term from the end in the expansion of (3√2+13√3)n is 16 then n is
9
6
12
none of these
The correct Answer is:a
Step by step video, text & image solution for If the ratio of 7th term from the beginning to the seventh term from the end in the expansion of (root(3)(2)+(1)/(root(3)(3)))^(n) is (1)/(6) then n is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Problem Set (1) (TRUE AND FALSE)4videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION
- BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Problem Set (1) (FILL IN THE BLANKS)3videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION
- BOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST16videos
AREA OF CURVES
- BOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - SELF ASSIGNMENT TEST11videos
CO-ORDINATE GEOMETRY OF THREE DIMENSION
Similar Questions
If the ratio of the 6th term from the beginning to the 6th term from the end in the expansion of (3√2+13√3)x is 16 then x=
View SolutionFind n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of (4√2+14√3)n is √6:1
View SolutionThe ratio of the fifth term from the beginning to the fifth term from the end in the expansion of (4√2+14√3)n is √6:1 If n=20λ, then the value of λ is
View SolutionFind the 4th term from the end in the expansion of (1−3x)10
View SolutionFind the 4th term from the end in the expansion of (1−3x)10
View SolutionFind n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of (4√2+14√3)nis √6:1.
View SolutionFind the 7th term from the end in the expansion of (x+1x)11
View SolutionFind the 7th term from the end in the expansion of (2x2−32x)8.
View SolutionRatio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of (21/3+12(3)1/3)10 is
View SolutionRatio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of (21/3+12(3)1/3)10 is
View Solution