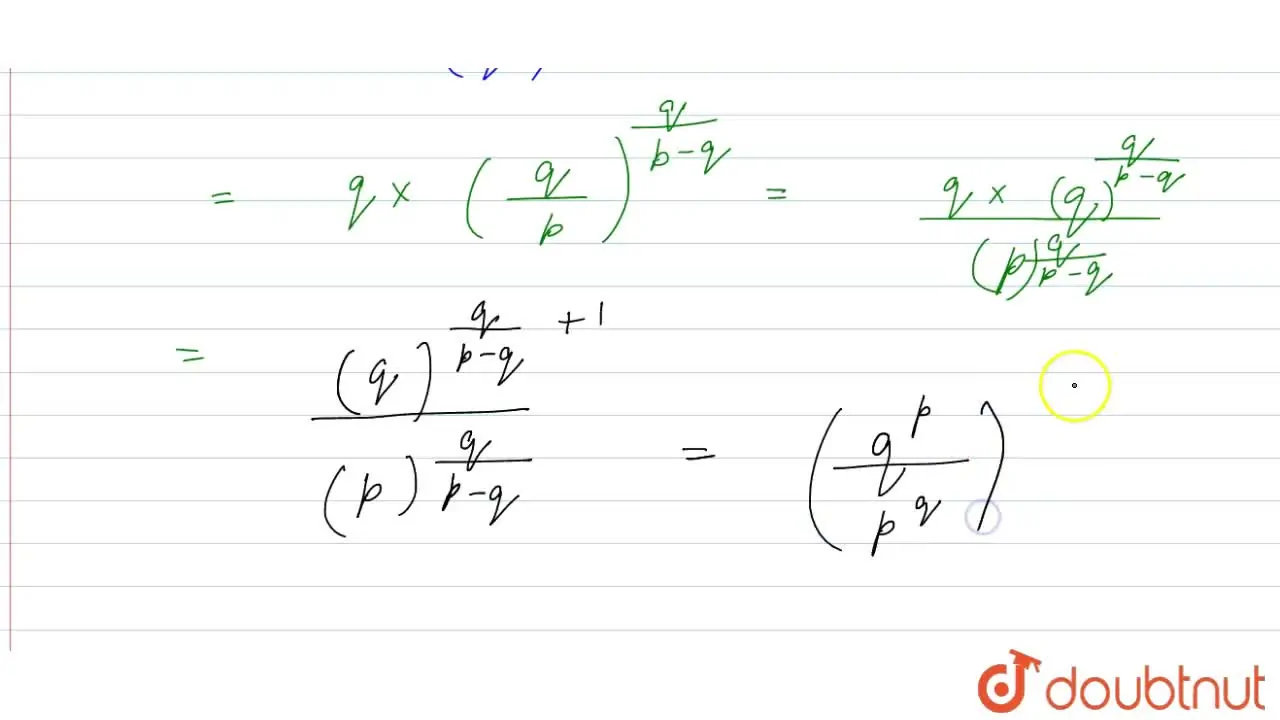If the terms of a G.P. are respectively, show that term is .
Let the first term and common ratio of GP be and r, respectively .
Accodring to the question , pth term = q
and q th term =p
On dividing Eq (i) by Eq (ii) We get
On substituting the value of r in Eq (i) , we get
Now (p+q) th term i.e.,
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - long answer type questions4videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Objective type Question10videos
SEQUENCE AND SERIES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False5videos
RELATIONS AND FUNCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE6videos
SETS
Similar Questions
If the pthandqth terms of a G.P. are qandp respectively, show that (p+q)th term is (qppq)1p−q .
View SolutionIf (p+q)thand (p−q)th terms of a G.P. re m and n respectively, then write it pth term.
View SolutionThe 5th, 8thand 11thterms of a G.P. are p, q and s, respectively. Show that q2=ps.
View SolutionIf (p+q)th term and (p−q)th terms of G.P. are a and b respectively, prove that pth term is √ab
View SolutionThe pth,qthand rthterms of an A.P. are a, b, c, respectively. Show that (q−r)a+(r−p)b+(p−q)c=0.
View SolutionIf the pth,qthand rthterms of a GP are a, b and c, respectively. Prove that aq−rbr−pcp−q=1.
View SolutionIf the pth ,qth and rth terms of a GP are a, b and c, respectively. Prove that aq−rbr−pcp−q=1 .
View SolutionThe (p+q)th term and (p-q)th terms of a G.P. are a and b respectively. Find the pth term.
View SolutionIf the pth, qth and rth terms of a G.P. are a, b, c respectively, prove that: a(q−r).ˆb(r−p).c(p−q)=1.
View SolutionIf pth, qth, and rth terms of an A.P. and G.P. are both a, b and c respectively show that ab−cbc−aca−b=1.
View Solution