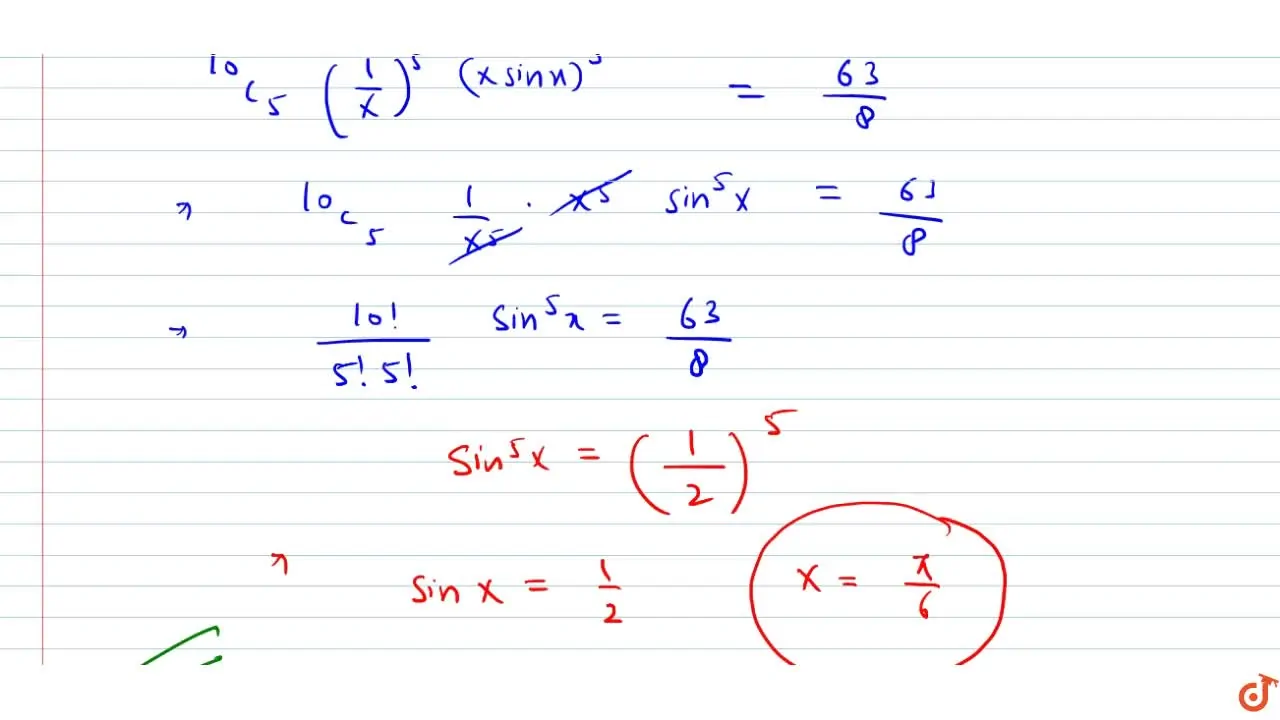If the middle term in the binomial expansion of (1x+xsinx10) is equal to 638, find the value of x.
(1x+xsinx)10
Middle term in the above expansion =102+1=6
Then,
T6=C(10,5)(1x)5(xsinx)5
⇒638=10⋅9⋅8⋅7⋅65⋅4⋅3⋅2⋅1sin5x
⇒18=4sin5x
⇒sin5x=132
⇒sinx=12
⇒x=π6
General value for x=nπ+(−1)nπ6,n∈Z.
Related Playlists
- BOOK - RD SHARMACHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Solved Examples And Exercises248videos
ARITHMETIC PROGRESSIONS
- BOOK - RD SHARMACHAPTER - BRIEF REVIEW OF CARTESIAN SYSTEM OF RECTANGULAR COORDINATESEXERCISE - Solved Examples And Exercises75videos
BRIEF REVIEW OF CARTESIAN SYSTEM OF RECTANGULAR COORDINATES
Similar Questions
If the middle term in the binomial expansion of (1x+xsinx10) is equal to 638, find the value of x.
View SolutionIf the middle term in the binomial expansion of (1x+xsinx)10 is 638 , then the value of 6sin2x+sinx−2 is
View SolutionFind the middle term in the expansion of (x+1x)4
View SolutionFind the middle term in the expansion of (x+1/x)9.
View SolutionFind the middle term in the expansion of (1+x)2n
View SolutionThe middle term in the expansioin of (1+x)2n is
View SolutionIf the middle term in the expansion of (1x+xsinx)10 is equal to 778, then the number of values of x in [0,2π] is equal to
View SolutionFind the middle term in the expansion of (x−12x)12
View SolutionFind the middle term in the expansion of (x+2)12.
View SolutionThe middle term in the expansion of(10x+x10)10 is :
View Solution