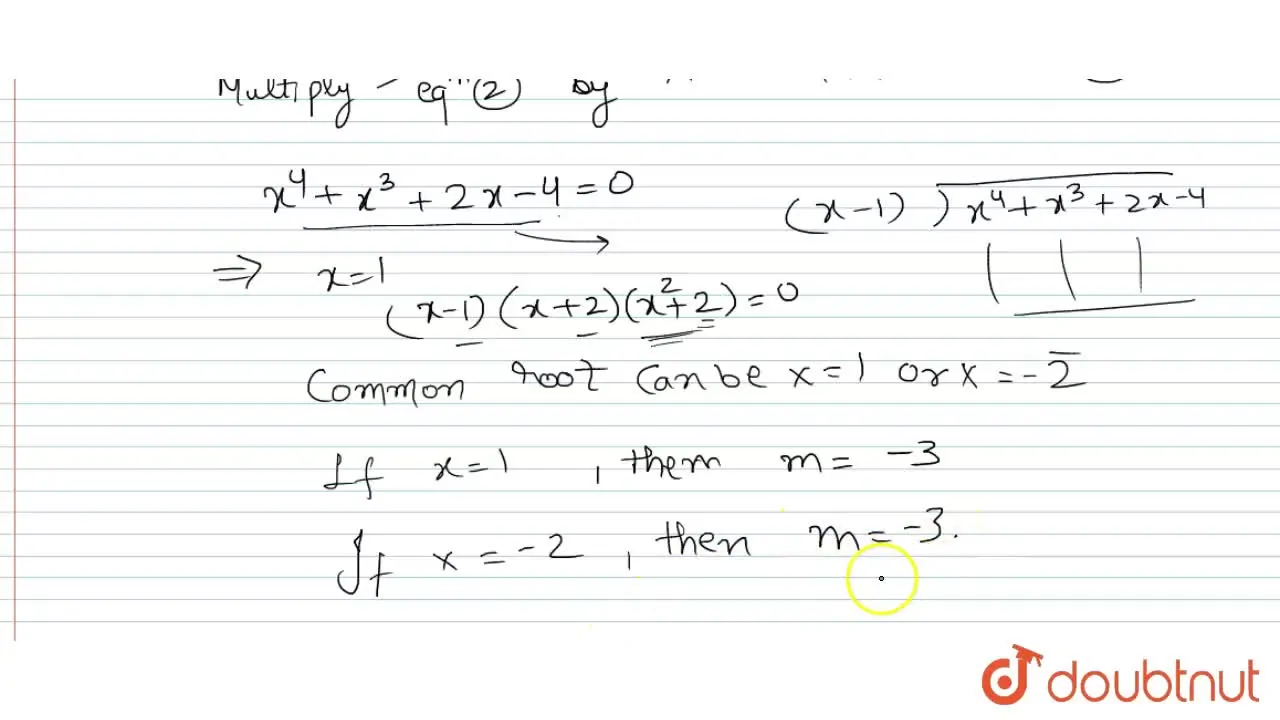If the equations x3−mx2−4=0andx3+mx+2=0.m∈R have one common root, then find the values of m.
The correct Answer is:-3
We have
x3−mx2−4=0 (1) and x3+mx+2=0 (2)
Multiplying (2) by x and adding with (1), we get
x4+x3+2x−4=0
⇒(x−1)(x+2)(x2+2)=0
So, common root can be x = 1 or x = -2
If x = 1 , then m = -3
If x = - 2 , then m = -3.
Related Playlists
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.118videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.1211videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.912videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank20videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If the equations x2+2x−3=0andx2+3x−m=0 have a common root, then the non- zero value of m.
View SolutionFind the sum of all the values of m so that , the equations 3x2−2mx−4=0 and x2−4mx+2=0" may have a common root.(" Can the equations have a common nonreal root)
View SolutionFor the two equations x2+mx+1=0andx2+x+m=0 , what is the value of m for which these equations have at least one common root?
View SolutionIf x2+4ax+3=0and2x2+3ax−9=0 have a common root, then the value of a, the common root are
View SolutionFor the two equations x2+mx+1=0andx2+x+m=0. What is/are the value/values of m for which these equations have at least one common root ?
View SolutionFind the value of λ so that the equations x2−x−12=0 and λx2+10x+3=0 may have one root in common. Also, find the common root.
View SolutionIf x=2 and x=3 are roots of the equation 3x2−mx+2n=0, then find the values of m and m.
View SolutionIf he roots of the equation12x2−mx+5=0 are in the ratio 2:3 then find the value of m.
View SolutionIf the equation x2−2mx+7m−12=0 has equal roots, then m=
View SolutionDetermine the values o m for which equations 3x2+4mx+2=0and2x2+3x−2=0 may have a common root.
View Solution