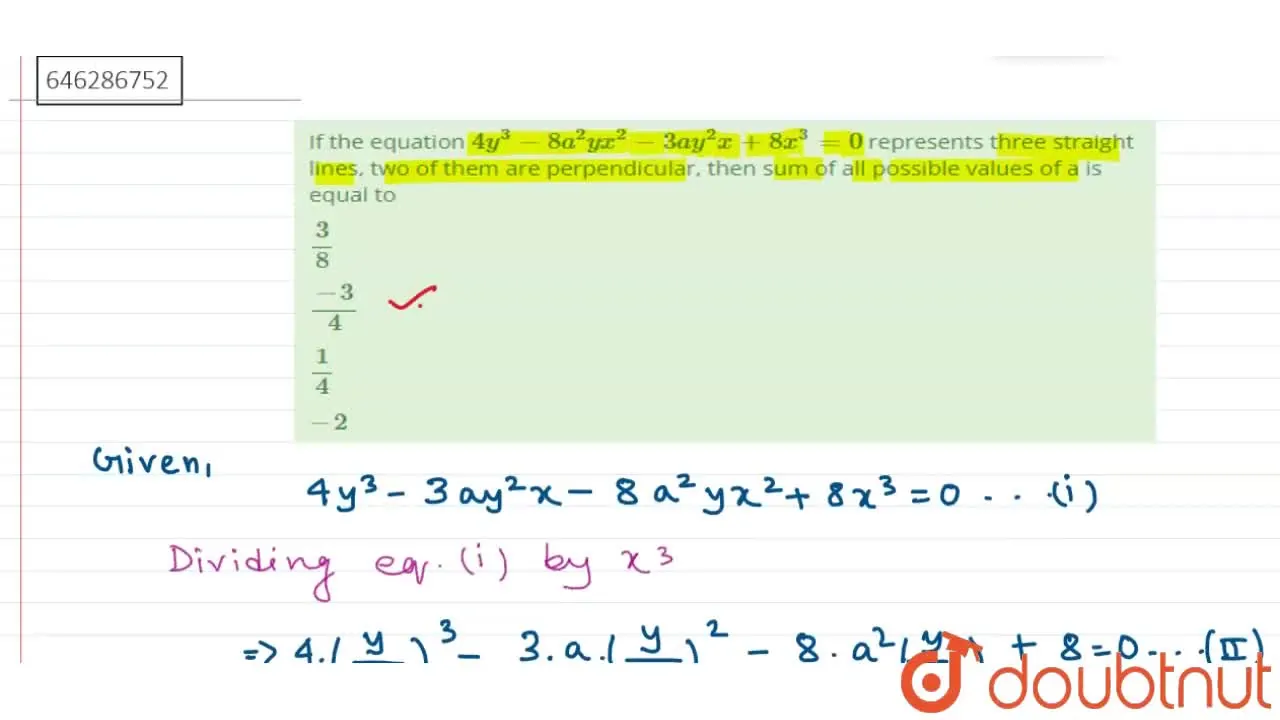
If the equation $4 y^{3} - 8 a^{2} y x^{2} - 3 a y^{2} x + 8 x^{3} = 0$ represents three straight lines, two of them are perpendicular, then sum of all possible values of a is equal to Solution in Bengali

A

$\frac{3}{8}$

B

$\frac{- 3}{4}$

C

$\frac{1}{4}$

D

$- 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

We have $4 y^{3} - 8 a^{2} y x^{2} - 3 a y^{2} x + 8 x^{3} = 0$
$\Rightarrow 4 {(\frac{y}{x})}^{3} - 3 a {(\frac{y}{x})}^{2} - 8 a^{2} (\frac{y}{x}) + 8 = 0$ has roots $m_{1}, m_{2}, m_{3}$
$∴ m_{1} m_{2} m_{3} = - 2$
Given $m_{1} m_{2} = - 1$
$∴ m_{3} = 2$
$∴ 4 {(2)}^{3} - 3 a {(2)}^{2} - 8 a^{2} (2) + 8 = 0$
$\Rightarrow 4 a^{2} + 3 a - 10 = 0$
$∴$ Sum of possible values of roots $= \frac{- 3}{4}$

|

Class 12 MATHS PAIR OF STRAIGHT LINES

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile