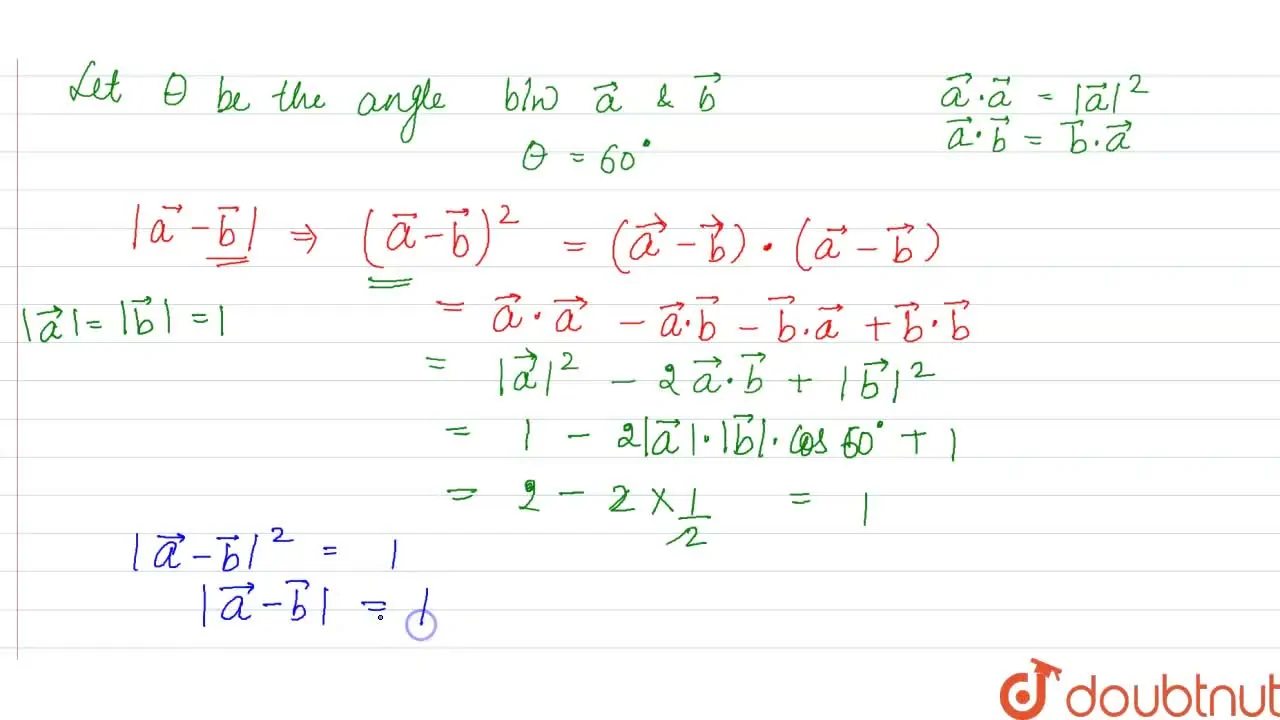If the angle between unit vectors →aand→bis60∘ . Then find the value of ∣∣→a−→b∣∣.
∣∣→a−→b∣∣2=(→a−→b).(→a−→b)
=a2+b2−2(→a.→b)
1+1−2(1.1.cosθ)
2(1−12)=1
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.215videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.318videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - True and false3videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions1344videos
CONIC SECTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - All Questions691videos
LIMITS AND DERIVATIVES
Similar Questions
If |→a|=3,∣∣→b∣∣=4 and the angle between →aand→bis120∘ . Then find the value of ∣∣4→a+3→b∣∣
View SolutionIf |→a|=3,∣∣→b∣∣=4 and the angle between →aand→bis120∘ . Then find the value of ∣∣4→a+3→b∣∣
View SolutionLet →a,→b,→c be three unit vectors and →a.→b=→a.→c=0 . If the angle between →band→c is π3 then find the value of ∣∣[→a→b→c]∣∣
View SolutionIf →a,→b,→c are unit vectors such that →a.→b=0=→a.→c and the angle between →band→cisπ3 , then find the value of ∣∣→a×→b−→a×→c∣∣
View SolutionThe angle between the two vectors →a+→b and →a−→b is
View SolutionIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
View SolutionLet →aand→b be unit vectors such that ∣∣→a+→b∣∣=√3. Then find the value of (2→a+5→b).(3→a+→b+→a×→b)
View SolutionFind the angle between unit vector →a and →b so that √3 →a - →b is also a unit vector.
View SolutionFind the angle between unit vector →a and →b so that √3 →a - →b is also a unit vector.
View SolutionFind the angle between unit vector →a and →b so that √3 →a - →b is also a unit vector.
View Solution