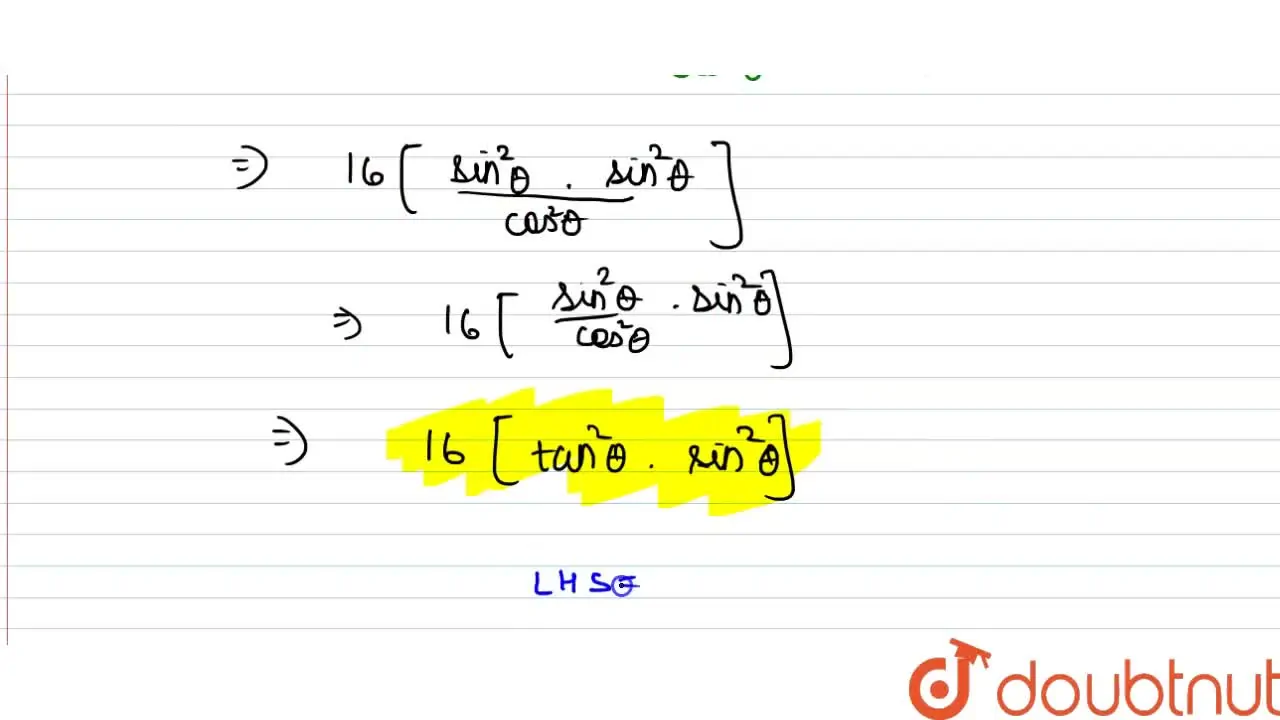
If (tanθ+sinθ)=mand(tanθ−sinθ)=n, prove that (m2−n2)2=16mn.
Step by step video & image solution for If (tan theta + sin theta) =m and (tan theta - sin theta) = n, prove that (m^(2)-n^(2))^(2)=16mn. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13C40videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Multiple Choice Questions (Mcq)53videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Exercise 13A38videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 1035videos
TRIGONOMETRIC RATIOS
Similar Questions
If cotx(1+sinx)=4mandcotx(1−sinx)=4n, prove that (m2−n2)2=mn .
View SolutionIf tanθ+sinθ=1, thencos2θ=n thenm2−n2 is equal
View SolutionIf tanθ+sinθ=m and tanθ−sinθ=n then prove m2−n2=4√mn
View SolutionIf tanθ+sinθ=m , tanθ−sinθ=n then m2−n2 is equal
View SolutionIf tanθ+sinθ=m and tanθ−sinθ=n, then m2−n2=
View SolutionIf acosθ+bsinθ=m and asinθ−bcosθ=n , prove that a2+b2=m2+n2
View SolutionIf tanθ+sinθ=mandtanθ−sinθ=n, then find the value of m2−n2.
View SolutionIf sinθ+cosθ=mandsecθ+cosecθ=n, prove that
n(m2−1)=2m.View SolutionIf acosθ+bsinθ=m and asinθ−bcosθ=n, Prove that a2+b2=m2+n2
View SolutionIf cotθ+cosθ=m and cotθ−cosθ=n then prove that: m2−n2=4√mn
View Solution