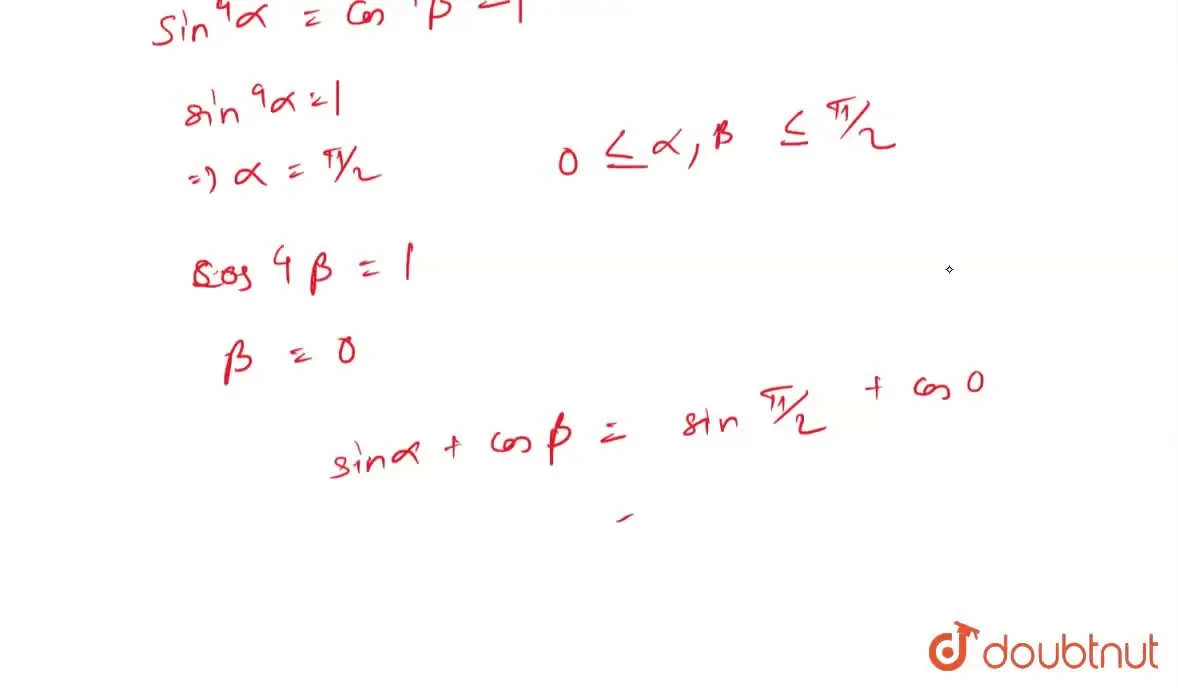If sin4α+cos4β+2=4sinαcosβ,0≤α,β≤π2 then find the value of (sinα+cosβ).Solution in Bengali
sin4α+sin4β+2=4sinαcosβ
We can write the above equation as,
(sin2α−1)2+(cos2β−1)2+(sinα−cosβ)2=0
⇒sin2α=1andcos2β=1andsinα=sinβ
As, αandβ in between 0 and π2,
∴sinα=cosβ=1
∴sinα+cosβ=1+1
⇒sinα+cosβ=2.
Related Playlists
Similar Questions
The pair of lines joining the origin to the points of intersection of the curves
ax2+2hxy+by2+2gx=0 and
a'x2+2h'xy+b'y2+2g'x=0
will be at right angles to one another , if04:05View SolutionProve that ∣∣ ∣ ∣∣cosαcosβcosαsinβsinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣=cos2α
05:30View Solutioncosα+cosβ=cos3π7 এবং sinα+sinβ=sin3π7 হলে, 2cos2α−β2-এর মান হবে-
08:59View Solutioncos4αcos2β+sin4αsin2β=1எனில் sin4α+sin4β=2sin2αsin2βஎன நிறுவுக
06:36View Solutioncos4αcos2β+sin4αsin2β=1எனில்cos4βcos2β+sin4βsin2α= என நிறுவுக
05:02View SolutionIf sin4α+cos4β+2=4sinαcosβ,0≤α,β≤π2 then find the value of (sinα+cosβ).
05:28View SolutionMinimum value of sec4αtan2β+sec4βtan2α, where α≠π2,β≠π2,0
09:49View SolutionIf cos4αcos2β+sin4αsin2β=1 prove that (i) sin4α+sin4β=2sin2αsin2β (ii) cos4βcos2α+sin4βsin2α=1
03:16View SolutionIf sin(α+β)=1 and sin(α−β)=12, where 0≤α,β≤π2 , then find the values of tan(α+2β) and tan(2α+β) .
05:44View SolutionIf α,βε(0,π2) and if sin4α+4cos4β+2=4√2sinαcosβthen the value of cos(α+β)−cos(α−β) is (A) √2 (B) 1√2 (C) −1√2 (D) −√2
03:42View SolutionIf cosα=35,cosβ=513,0<α,β<π2 then find the value of sin2(α−β2)andcos2(α−β2).
05:06View SolutionIf A= [{:(cos alpha,sinalpha),(-sin alpha,cos alpha):}] is, then A^(2) The value of -
05:45View SolutionIf 0<β<α<(π4),cos(α+β)=35 and cos(α−β)=45 then find the avlue of sin2α
03:13View SolutionIf sinα,sin2α,1,sin4αandsin6α are in A.P., where −π<α<π, then α lies in the interval
04:38View SolutionIf cos4αcos2β+sin4αsin2β=1,then prove that
sin4α+sin4β=2sin2αsin2β.06:59View SolutionIf cos4αcos2β+sin4αsin2β=1,then prove that
cos4βcos2α+sin4βsin2α=102:59View Solution