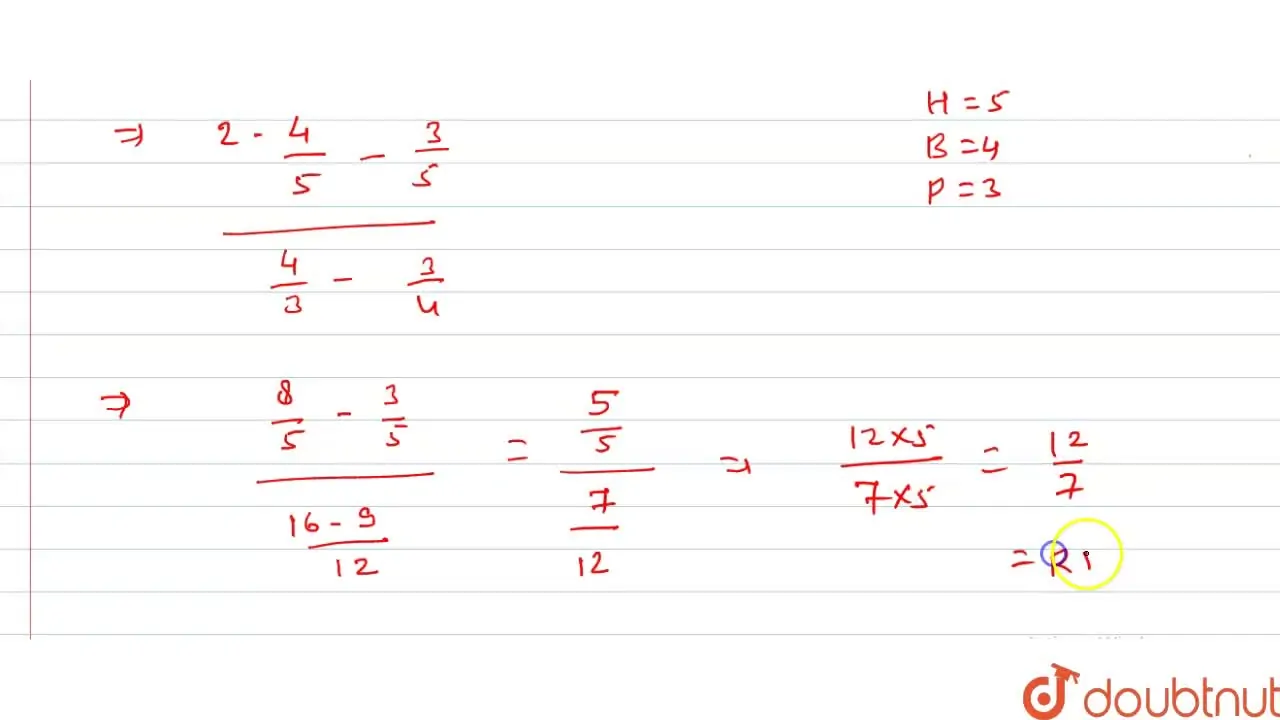If secθ=54,find the value of (2cosθ−sinθ)(cotθ−tanθ)=.
A
(12)/(7)
B
(12)/(5)
C
(1)/(7)
D
(2)/(5)
Video Solution
Text Solution
The correct Answer is:A
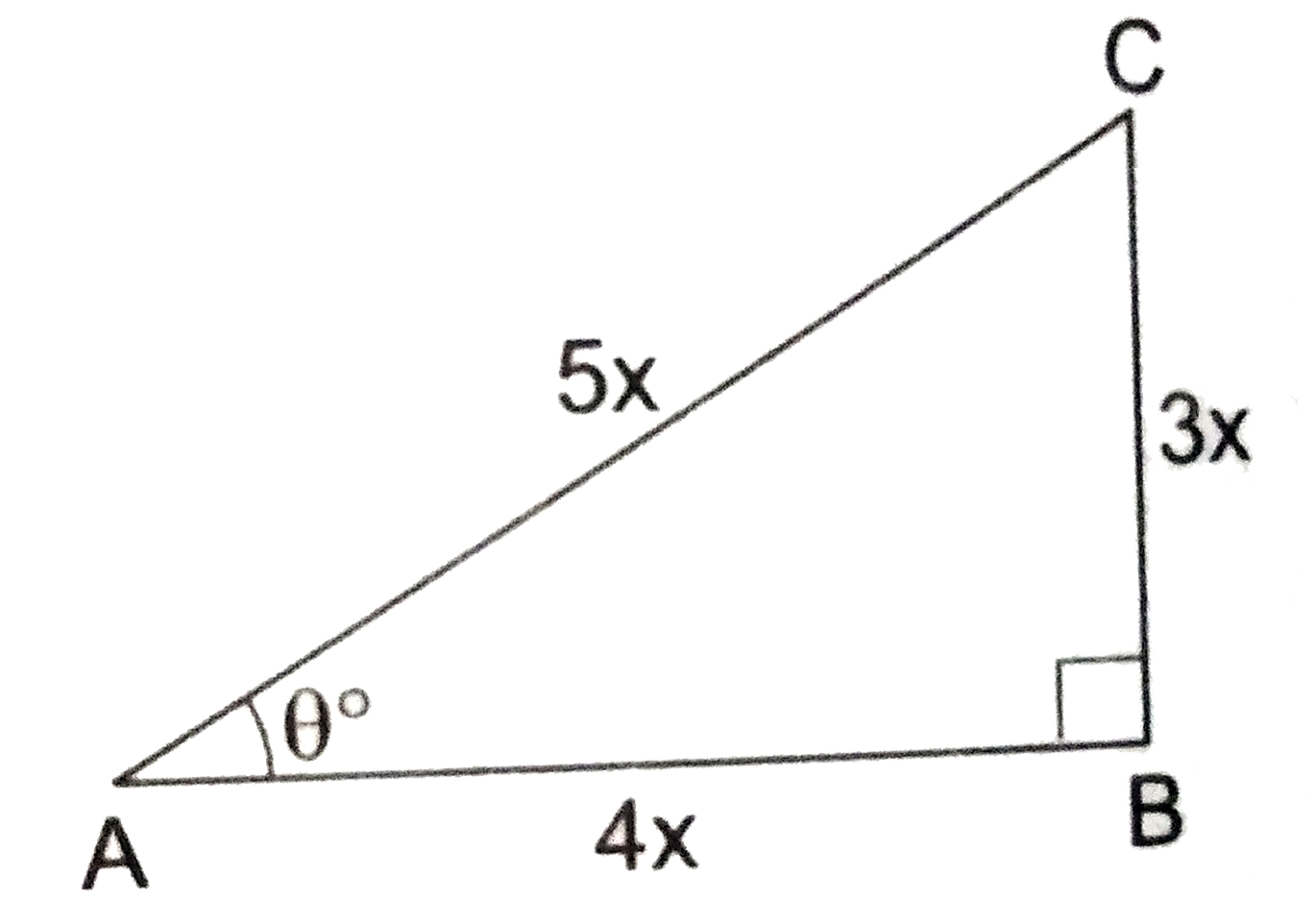
Consider a ΔABCin which ∠A=θand∠B=90∘.
secθ=hypotenusebase=ACAB=54=5x4x(say)
∴AC=5xandAB=4x,wherex is positive .
By pythagoras' theorem we have
AC2=AB2+BC2
⇒BC2=AC2−AB2=(5x)2−(4x)2=9x2
⇒BC=3x.
∴cosθ=ABAC=4x5x=45,sinθ=BCAC=3x5x=35,
cotθ=ABBC=4x3x=43,andtanθ=BCAB=3x4x=34.
∴(2cosθ−sinθ)(cotθ−tanθ)=(2×45−35)(43−34)=(85−35)(43−34)=(55)(712)=1(712)=127.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - Exercise 1035videos
TRIGONOMETRIC RATIOS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 1215videos
TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES
Similar Questions
If cosθ=35,find the value of (5cosec θ−4tanθsecθ+cotθ).
View SolutionIf secθ=54 , find the value of sinθ−2cosθtanθ−cotθ
View SolutionIf tanθ=45, find the value of cosθ−sinθcosθ+sinθ .
View SolutionIf sinθ=5/13, then find the value of (cotθ−tanθ)/2cotθ ?
View SolutionIf cosecθ=√5/2, find the value of secθ+tanθ−cotθ.
View SolutionIf 3cotθ=4,find the value of 4cosθ−sinθ2cosθ+sinθ .
View SolutionIf 3tanθ=4 , find the value of 4cosθ−sinθ2cosθ+sinθ
View SolutionIf 5cotθ=3, find the value of (5sinθ−3cosθ4sinθ+3cosθ).
View SolutionIf tanθ=34 then find the values of secθ and cosθ
View SolutionIf sinθ=45 , find the value of 4tanθ−5cosθsecθ+4cotθ
View Solution