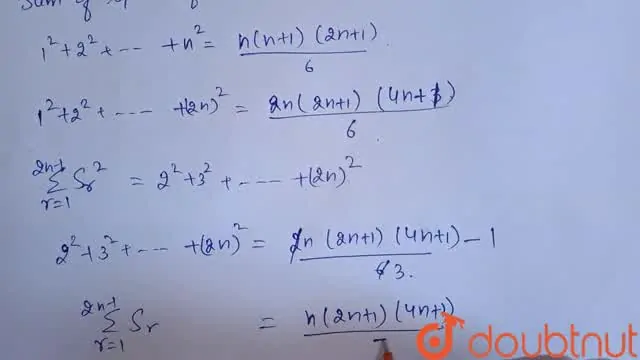If S1,S2,S3,.........Sn,........ are the sums of infinite geometric series whose first terms are 1,2,3............n,............. and whose common ratio 12,13,14,........,1n+1,....respectively, then find the value of 2n−1∑r=1S21.
Step by step video & image solution for If S_1, S_2 ,S_3,.........S_n,........ are the sums of infinite geometric series whose first terms are 1,2,3............n,............. and whose common ratio 1/2,1/3,1/4,........,1/(n+1),....respectively, then find the value of sum_(r=1)^(2n-1) S_1^2. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
If S1,S2,S3,...,Sn are the sums of infinite geometric series, whose first terms are 1, 2, 3,.., n and whose common rations are 12,13,14,...,1n+1 respectively, then find the values of S21+S22+S23+...+S22n−1.
View SolutionIf S1,S2,S3,......,Sp are the sums of infinite geometric series whose first terms are 1, 2, 3..... p and whose common ratios are 12,13,....1p+1 respectively, prove that
S1+S2+S3+....+Sp=12p(p+3) .View SolutionIf S1,S2,S3…….,S2n are the sums of infinite geometric series whose first terms are respectively 1,2,3,…..,2n and common ratio are respectively,
12,13,……..,12n+1, find the value of ,S21+S22+…....+S22n−1.View SolutionIf S1,S2,S3,…..,Sn are the sum of infinite geometric series whose first terms are 1,3,5….,(2n−1) and whose common rations are 23,25,….,22n+1 respectively, then {1S1S2S3+1S2S3S4+1S3S4S5+.........upon infinite terms}=
View SolutionFind the sum of the following series whose nth term is: 2n3+3n2−1.
View SolutionIf 1+ab+a2b2+a3b3+...+∞=xyx+y−1 are the sum of infinire geometric series whose first terms are 1,2,3,….,p and whose common ratios are S1,S2,S3,....,Sp12,13,14,...1p+1 respectively, prove that S1+S2+S3+....+Sp=p(p+3)2.
View SolutionS1,S2,S3,...,Sn are sums of n infinite geometric progressions. The first terms of these progressions are 1,22−1,23−1,...,2n–1 and the common ratios are 12,122,123,....,12n. Calculate the value of S1,+S2,+...+Sn.
View SolutionIf S1,S2,S3,Sm are the sums of n terms of m A.P. 's whose first terms are 1,2,3,....m and common differences are 1,3,5,....(2m−1) respectively. Show that S1+S2.....+Sm=mn2(mn+1)
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionIf S1,S2,S3,Sm are the sums of n terms of m A.P. 's whose first terms are 1,2,3,,m and common differences are 1,3,5,,(2m−1) respectively. Show that S1+S2,+Sm=mn2(mn+1)
View Solution