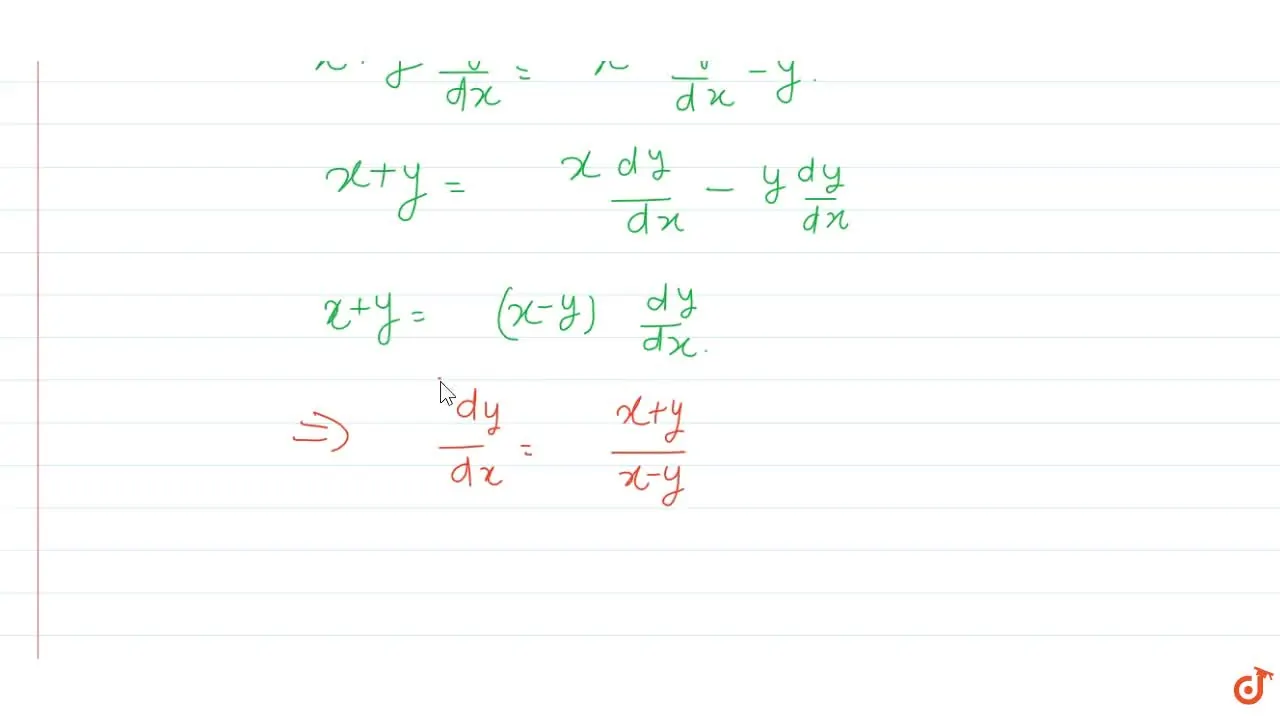If log√(x2+y2)=tan−1(yx), show that dydx=x+yx−y
Video Solution
Text Solution
Given that, $$ \log \sqrt{x^{2}+y^{2}}=\tan ^{-1}\left(\frac{y}{x}\right) $$ Prove that, $$ \begin{gathered} \frac{d y}{d x}=\frac{x+y}{x-y} \\ \Rightarrow \frac{1}{2} \log \left(x^{2}+y^{2}\right)=\tan ^{-1}\left(\frac{y}{x}\right) \quad\left[\frac{d}{d x}(\log x)=\frac{1}{x}\right] \\ \Rightarrow \frac{1}{2}\left(\frac{1}{x^{2}+y^{2}}\left(2 x+2 y \frac{d y}{d x}\right)\right)=\frac{1}{1+\left(\frac{y}{x}\right)^{2}}\left(\frac{x \frac{d y}{d x}-y}{x^{2}}\right) \\ \frac{2\left(x+y \frac{d y}{d x}\right)}{2\left(x^{2}+y^{2}\right)}=\frac{x^{2}}{x^{2}+y^{2}}\left(\frac{x \frac{d y}{d x}-y}{x^{2}}\right) \\ \frac{d y}{d x}(y-x)=-y-x . \\ \frac{d y}{d x}=\frac{x+y}{x-y} \end{gathered} $$ Hence proved
|
Updated on:21/07/2023
Related Playlists
- BOOK - RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Solved Examples And Exercises102videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - RD SHARMACHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Solved Examples And Exercises67videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
If log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y .
View SolutionIf log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y
View SolutionIf log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y
View SolutionIf log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y
View SolutionIf log (x2+y2)=tan−1 (yx), then show that dydx=x+yx−y
View SolutionIf log√x2+y2=tan−1(yx),thendydx is
View SolutionIf log(x2+y2)=2tan−1(xy) then show that dydx=y−xy+x
View Solutionif y=√x2+a2, then show that ydydx=x
View SolutionIf x=log(1+t2),y=t−tan−1t, show that dydx=√ex−12
View SolutionIf y=log{√x−1−√x+1} , show that dydx=−12√x2−1
View Solution