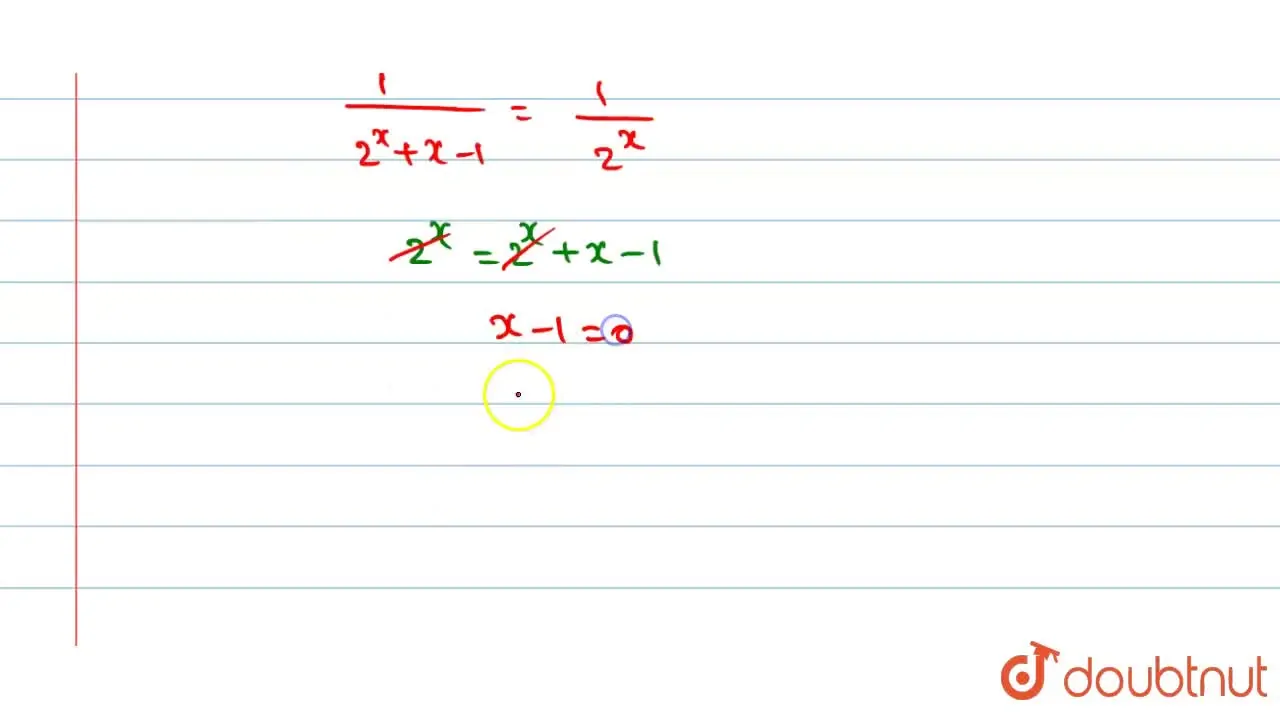If (log)10[12x+x−1]=x[(log)105−1] , then x= 4 (b) 3 (c) 2 (d) 1
4
3
2
1
The correct Answer is:D
R.H.S. = x=[log105−log1010]=xlog10.510=log10.12x
⇒12x+x−1=12x
Therefore x−1=0orx=1.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - Multiple Correct Answers Type18videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - Linked Comprehension Type6videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - Exercise 1.66videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGE ENGLISHCHAPTER - LOGARITHM AND ITS APPLICATIONS EXERCISE - Subjective Type9videos
LOGARITHM AND ITS APPLICATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
Similar Questions
If 1logx10=2loga10−2, then x =
View Solution(log)10(x−3)(log)10(x2−21)=12then find x.
View Solution(log)x−1x(log)x−2(x−1).....(log)x−12(x−11)=2,x is equal to: 9 (b) 16 (c) 25 (d) none of these
View SolutionIf S={x∈N:2+(log)2√x+1>1−(log)12√4−x2} , then (a)S={1} (b) S=Z (c) S=N (d) none of these
View SolutionIf (log)3{5+4(log)3(x−1)}=2, then x is equal to 4 (b) 3 (c) 8 (d) (log)216
View SolutionIf (log)3{5+4(log)3(x−1)}=2, then x is equal to 4 (b) 3 (c) 8 (d) (log)216
View SolutionIf y=tan−1{(log)e(e/x2)(log)e(ex2)}+tan−1(3+2 (log)ex1−6 (log)ex) , then d2ydx2= (a) 2 (b) 1 (c) 0 (d) -1
View Solutionif x+log10(1+2x)=xlog105+log106 then x
View SolutionGiven system of simultaneous equations 2x .5y=1 and 5x+1.2y=2. Then - (a) . x=(log)105 and y=(log)102 (b) . x=(log)102 and y=(log)105 (c) . x=(log)10(15) and y=(log)102 (d) . x=(log)105 and y=(log)10(12)
View SolutionIf 53x2log102=2(x+12)log1025, then x equals to
View Solution