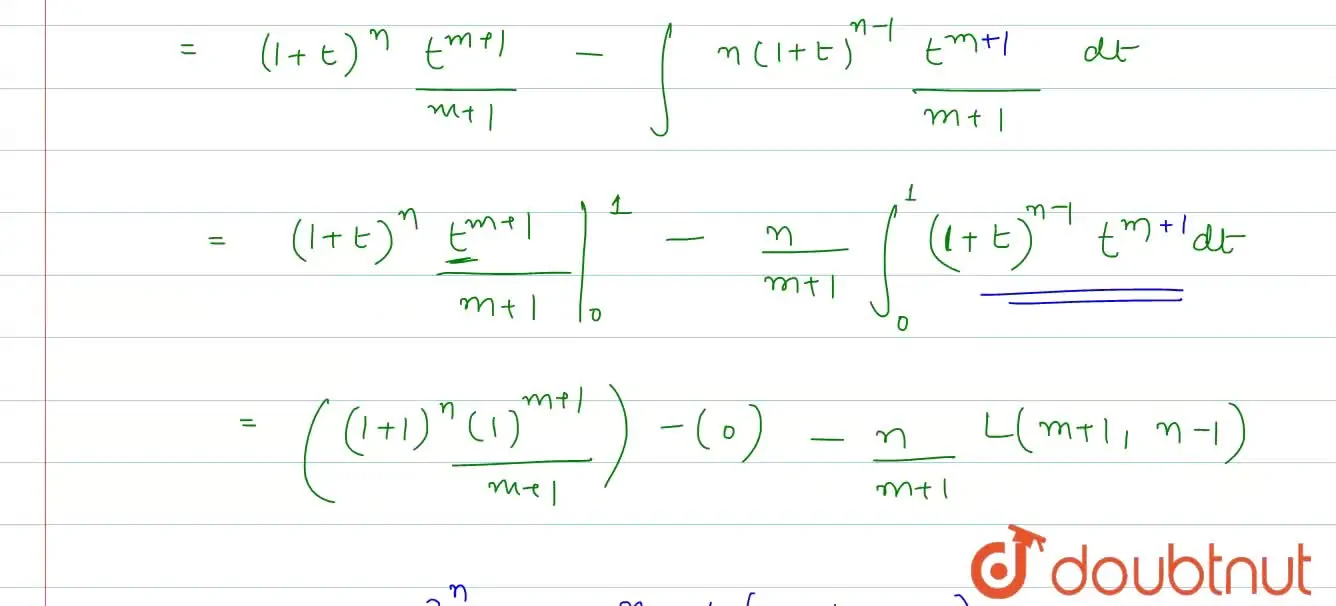If L(m,n)=∫10tm(1+t)n,dt, then prove that
L(m,n)=2nm+1−nm+1L(m+1,n−1)
The correct Answer is:NA
L(m,n)=∫10tm(1+t)ndx
=[tm+1m+1(1+t)n]10−∫10n(1+t)n−1tm+1m+1dx
=[tm+1m+1(1+tn)]10−nm+1∫10tm+1(1+t)n−1dx
2nm+1−nm+1L(m+1,n−1)
Related Playlists
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise (Single)113videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise (Multiple)27videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - DEFINITE INTEGRATION EXERCISE - Exercise 8.107videos
DEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - CURVE TRACINGEXERCISE - Exercise24videos
CURVE TRACING
- BOOK - CENGAGECHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer5videos
DETERMINANT
Similar Questions
If I(m,n)=∫10tm(1+t)n.dt, then the expression for I(m,n) in terms of I(m+1,n-1) is:
View SolutionIf I(m,n)=∫10tm(1+t)ndt,m,n,∈R , then I (m,n) is
View SolutionIf lm,n=∫xmcosnxdx, then prove that lm,n=xmsinnxn+mxm−1cosnxn2−m(m−1)n2lm−2,n
View SolutionIf ln=∫emxcosnxdx then prove that (m2+n2)In=emx⋅(mcosx+nsinx)cosn−1x+n(n−1)ln−2
View SolutionIf a=xm+n y1, b−xn+l ym and c=xl+myn, prove that am−n bn−1 c1−m =1
View SolutionIfI(m,n)=∫10xm−1(1−x)n−1dx,(m,n∈I,m,n≥0),then I(m,n)=∫∞0xm−1(1+x)m−ndx I(m,n)=∫∞0xm−1(1+x)m+ndx I(m,n)=∫∞0xn−1(1+x)m+ndx I(m,n)=∫∞0xn(1+x)m+ndx
View Solution∫10x(m−1)(1−x)(n−1)dx is equal to where m,n∈N
View SolutionLet m,n be two positive real numbers and define f(n)=∫∞0xn−1e−xdx and g(m,n)=∫10xm−1(1−m)n−1dx.
It is known that f(n) for n gt 0 is finite and g(m, n) = g(n, m) for m, n gt 0.
∫∞0xm−1(1+x)m+ndx=View SolutionLet m,n be two positive real numbers and define f(n)=∫∞0xn−1e−xdx and g(m,n)=∫10xm−1(1−m)n−1dx.
It is known that f(n) for n gt 0 is finite and g(m, n) = g(n, m) for m, n gt 0.
∫10xm(loge.1x)dx=View SolutionIf x=am+n,y=an+1andz=al+m , prove that xm+ynzl=xnylzm
View Solution