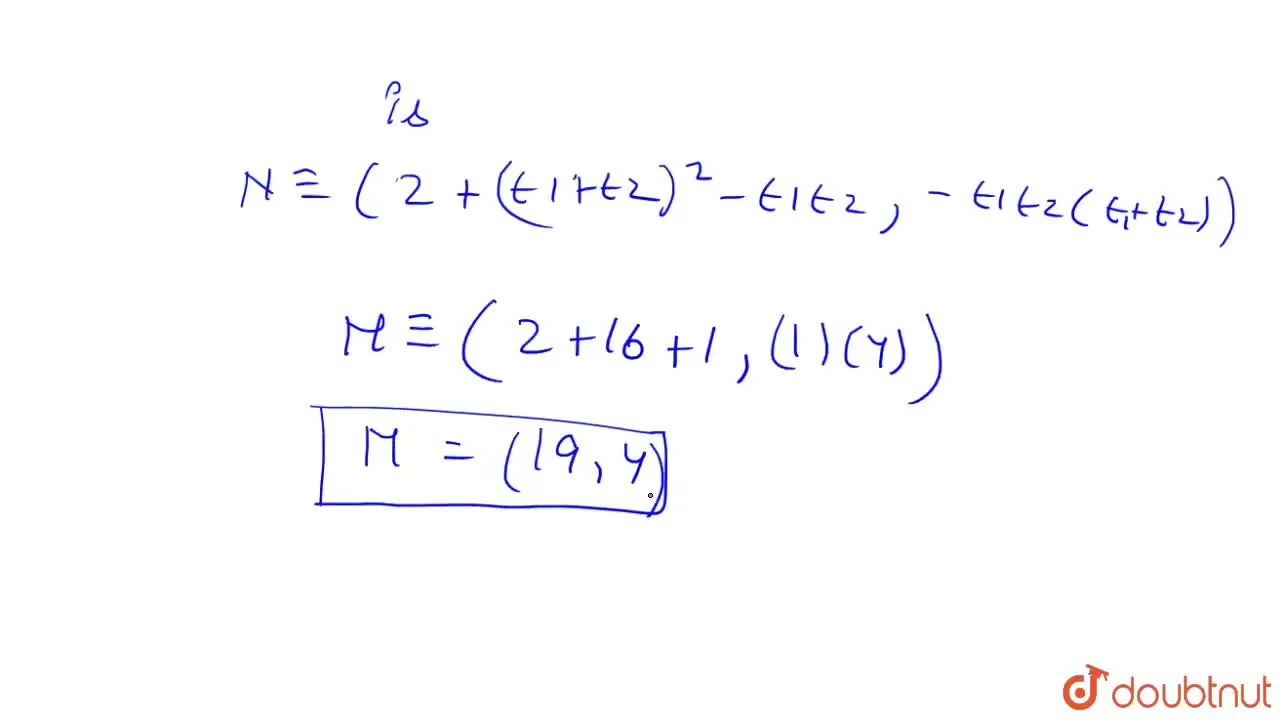If line x-2y-1=0 intersects parabola y2=4x at P and Q, then find the point of intersection of normals at P and Q.
The correct Answer is:(19,4)
Any equation on the parabola y2=4x, say (t2,2t), lies on the line x-2y-1=0.
∴ t2−4t−1=0
This equation has two roots t1andt2, which are parabola are parameters of the points of intersection of line and parabola.
∴ t1+t2=4andt1t2=−1
Now, point of intersection of normals at P and Q is
N≡(2+(t21+t22)+t1t2(t1+t2))
or N≡(2+(t1+t2)2−t1t2,−t1t2(t1+t2))
Putting the value of t1+t2andt1t2, we get
N≡(2+16+1,1(4))≡(19,4)
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Single)98videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)26videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.68videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
If the line x−y−1=0 intersect the parabola y2=8x at P and Q, then find the point on intersection of tangents PandQ.
View SolutionPoint of intersection of normal at P(at21,2at1) and Q(at22,2at2)
View SolutionIf normal of circle x2+y2+6x+8y+9=0 intersect the parabola y2=4x at PandQ then find the locus of point of intersection of tangent's at PandQ.
View SolutionThe line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
View SolutionIf PQ is the focal chord of the parabola y2=−xandP is (−4,2), then the ordinate of the point of intersection of the tangents at P and Q is
View SolutionIf the straight line x−2y+1=0 intersects the circle x2+y2=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x2+y2=25.
View SolutionIf the distances of two points P and Q from the focus of a parabola y2=4x are 4 and 9,respectively, then the distance of the point of intersection of tangents at P and Q from the focus is
View Solutionif a variable tangent of the circle x2+y2=1 intersects the ellipse x2+2y2=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View SolutionIf 3x+4y=12 intersect the ellipse x225+y216=1 at P and Q , then point of intersection of tangents at P and Q.
View SolutionThe ordinates of points P and Q on the parabola y2=12x are in the ration 1:2 . Find the locus of the point of intersection of the normals to the parabola at P and Q.
View Solution