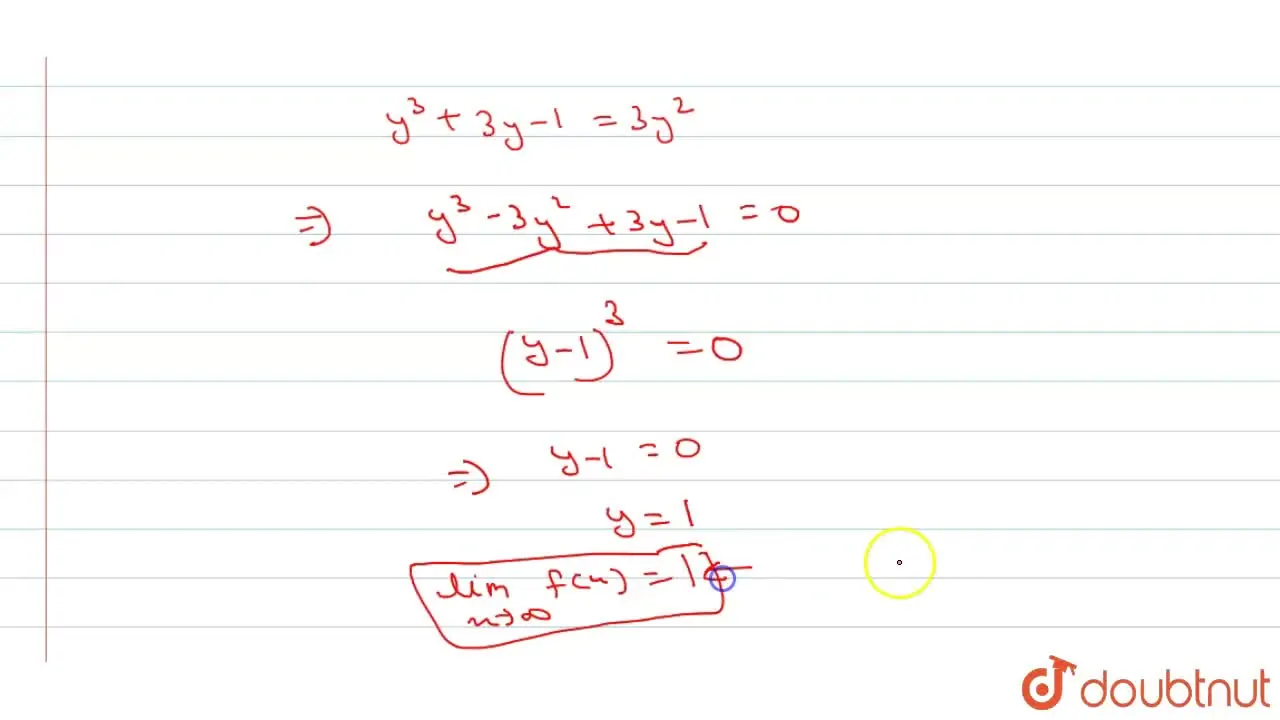If limx→∞f(x) exists and is finite and nonzero and if limx→∞{f(x)+3f(x)−1f2(x)}=3, then the value of limx→∞f(x) is _______.
Video Solution
Text Solution
The correct Answer is:(1)
limx→∞(f(x)+3f(x)−1f2(x))=3
or ⎛⎜
⎜⎝limx→∞f(x)+3limx→∞f(x)−1(limx→∞f(x))2⎞⎟
⎟⎠=3
or (y+3y−1y2)=3
or y3−3y2+3y−1=0
or (y−1)3=0
or y=1
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Archives JEE MAIN8videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Archives JEE ADVANCED2videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Matrix Match Type5videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
- BOOK - CENGAGE ENGLISHCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
Similar Questions
If limx→∞f(x) exists and is finite and nonzero and if limx→∞{f(x)+3f(x)−1f2(x)}=3,then the value of limx→∞f(x) is
View SolutionIf limx→0[1+x+f(x)x]1/x=e3, then the value of ln⎛⎝limx→0[1+f(x)x]1/x⎞⎠ is _________.
View SolutionIf x2+x−2x+3≤f(x)x2≤x2+2x−1x+3 hold for a certain interval containing the point x=−1 and limx→−1f(x) then find the value of limx→−1f(x)
View SolutionIf limx→∞{x2+1x+1−(ax+b)}=0, then find the values of a and b.
View SolutionEvaluate limx→∞(x−3x+2)x
View SolutionEvaluate limx→∞(x−3x+2)x
View SolutionIf limx→∞(x2+x+1x+1−ax−b)=4, then
View Solutionlimx→∞x(logx)31+x+x2 equals
View SolutionEvaluate limx→∞x1x.
View SolutionIf limx→a[f(x)+g(x)]=2 and limx→a[f(x)−g(x)]=1, then find the value of limx→af(x)g(x).
View Solution