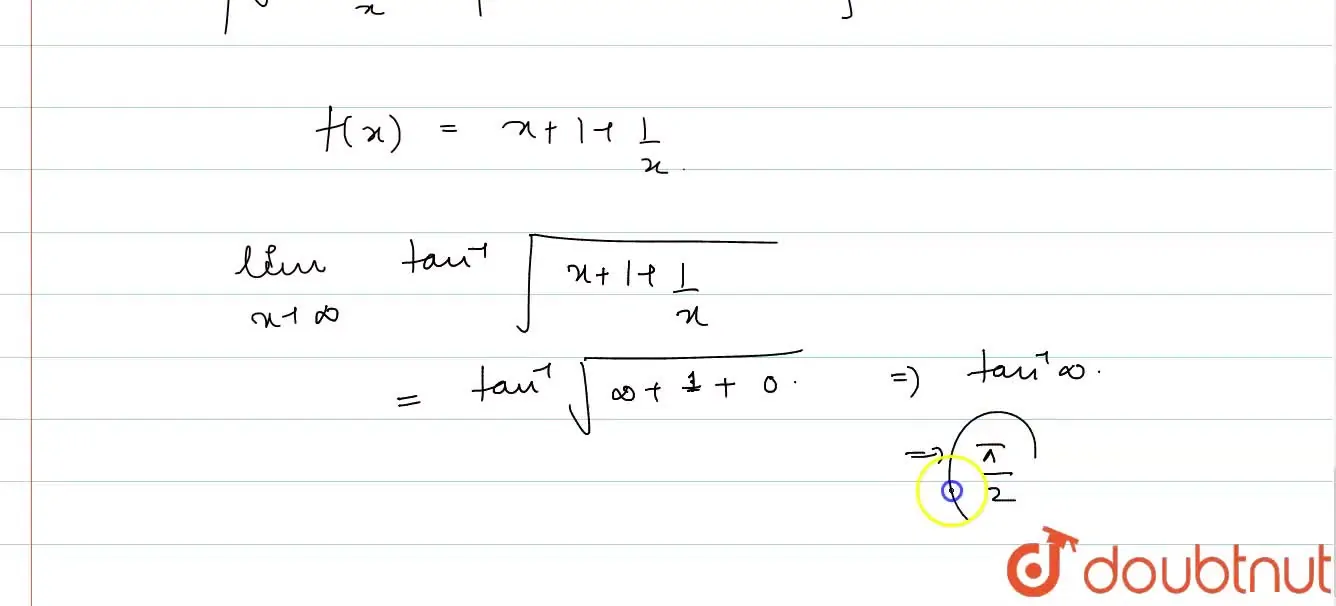If ∫x(x−1)(x2+1)(x+1)√x3+x2+xdx
=12loge∣∣
∣∣√f(x)−1√f(x)+1∣∣
∣∣−tan−1√f(x)+C, then
The value of limx→∞tan−1√f(x) is
A
π/2
B
π/4
C
π
D
2π
Video Solution
Text Solution
The correct Answer is:A
∫x(x−1)(x2+1)(x+1)√x3+x2+xdx
=∫x(x−1)(x2+1)(x+1)x√x+1+1xdx
=∫x2−1(x2+1)(x+1)2√x+1+1xdx
=∫1−1x2(x+1x)(x+2+1x)√x+1+1xdx
Put x+1x+1=t2
∴I=∫2tdt(t2−1)(t2+1)t
=2∫dt(t2−1)(t2+1)
=∫(1t2−1−1t2+1)dt
=12log∣∣∣t−1t+1∣∣∣−tan−1t+C
=12loge∣∣
∣
∣∣√x+1x+1−1√x+1x+1+1∣∣
∣
∣∣−tan−1√x+1x+1+C
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Matrix)4videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Numerical)10videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercise (Multiple)17videos
INDEFINITE INTEGRATION
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year14videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
Similar Questions
If ∫x(x−1)(x2+1)(x+1)√x3+x2+xdx
=12loge∣∣ ∣∣√f(x)−1√f(x)+1∣∣ ∣∣−tan−1√f(x)+C, then ,the value of f(1) isView SolutionLet f(x)=x+1x+2 . If ∫(f(x)x2)12dx=1√2g(√2f(x)−1√2f(x)+1)−h(√f(x)−1√f(x)+1) then
View SolutionIf ∫f(x)x2−x+1dx=32log(x2−x+1)+1√3tan−1(2x−1)√3+C then f(x) is equal to
View SolutionIf f(x)=∫2−11+x2−1√1+x2dx, then f is
View SolutionIf ∫x−1x2√2x2−2x−1dx= √f(x)g(x)+c then the value of f(x) and g(x) is
View Solutionf(x)=√1−sin2x+√1+tan2x then
View SolutionThe value if ∫x2−1(x2+1)(√x4+1)dx equal to 1√2sec−1(f(x))+c, then f(x) is
View SolutionIf f(x)=sin−1x+tan−1xπ+2√x, then the range of f(x) is
View SolutionIf f(x)=√1−√1−x2, then at x = 0
View SolutionIf f(x)=x(√x−√x+1) then f(x) is:
View Solution