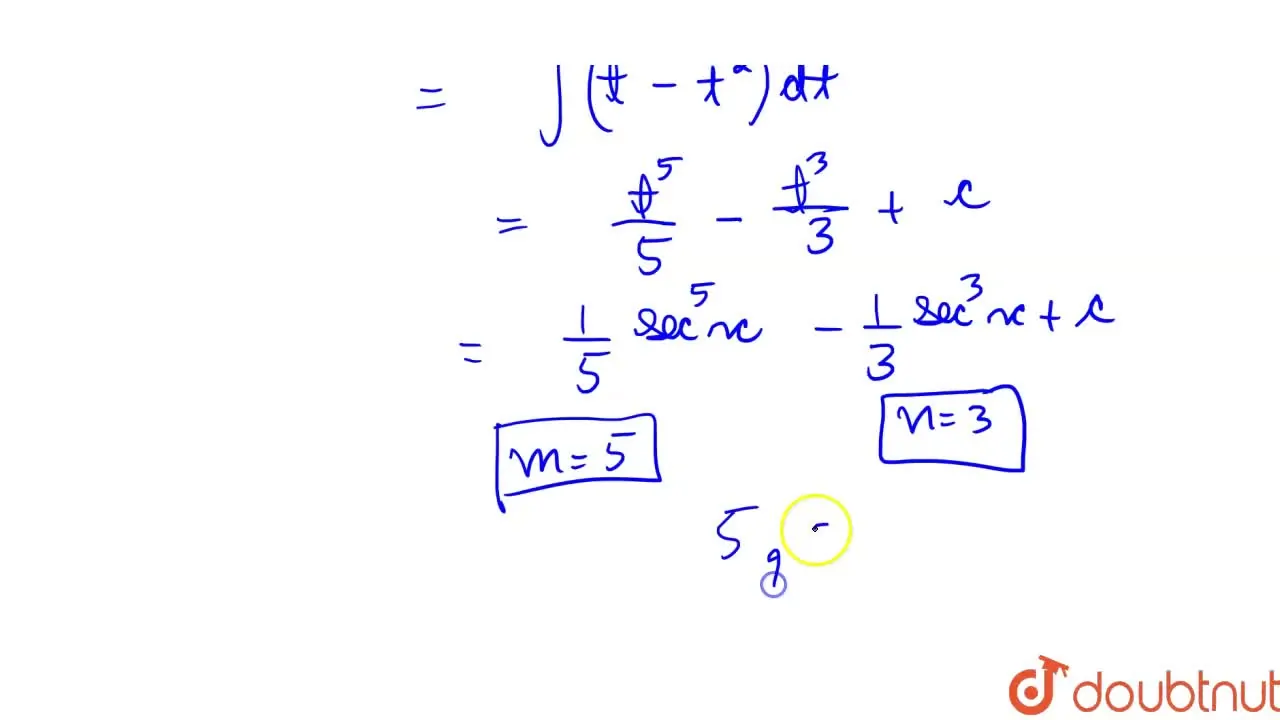If ∫tan3xsec3xdx=(1m)secmx−(1n)secnx+c, then (m,n)≡
A
(5,3)
B
(3,5)
C
(15,13)
D
(4,4)
Video Solution
Text Solution
The correct Answer is:A
|
Answer
Step by step video, text & image solution for If inttan^(3)x sec^(3)xdx=((1)/(m))sec^(m)x-((1)/(n))sec^(n)x+c, then (m, n)-= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - INDEFINITE INTEGRALSEXERCISE - MULTIPLE CHOICE QUESTIONS(PART - B : Mastering The BEST)327videos
INTEGRATION - INDEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - INDEFINITE INTEGRALSEXERCISE - MULTIPLE CHOICE QUESTIONS (PREVIOUS YEARS MHT-CET EXAM QUESTIONS)13videos
INTEGRATION - INDEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - LINE IN SPACE EXERCISE - MULTIPLE CHOICE QUESTIONS44videos
LINE IN SPACE
Similar Questions
∫tanmxsec2xdx
View Solution∫(1+tan3x)sec2xdx=
View SolutionIf ∫sin4xcos3xdx=1msinmx−1nsinnx+c then (m,n)≡
View Solution∫xsinxsec3xdx
View Solution∫sec2xcos3xdx=
View Solution" () "int tan^(3)x*sec xdx
View Solution" (3) "int tan^(3)x*sec xdx
View Solution∫xsec−1xdx
View Solution∫sec(tanx)⋅sec2xdx
View Solution∫sec43xtanxdx
View Solution