If f(y)=⎧⎪⎨⎪⎩(e2y−1)⋅sinyy2, for y≠04, for y=0, then f(y) is
A
discontinuous at y = 0
B
continuous at y = 0
C
not defined
D
None of the above
Video Solution
Text Solution
The correct Answer is:A
Given, f(y)=⎧⎪⎨⎪⎩(e2y−1)sinyy2,y≠04,y=0
Now limy→0f(y)=limy→0(e2y−1)2y×2×sinyy
=loge×2×1=2 but f(0)=4
∴f(0)≠limy→0f(y)
Hence, f(y) is discontinuous at y = 0
|
Topper's Solved these Questions
- CONTINUITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CONTINUITYExercise:MHT CET Corner
Explore 16 Videos
- CONTINUITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CONTINUITYExercise:MHT CET Corner
Explore 16 Videos
- CIRCLE AND CONICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CIRCLE AND CONICSExercise:All Questions
Explore 74 Videos
- DEFINITE INTEGRALSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:DEFINITE INTEGRALSExercise:MHT CET Corner
Explore 22 Videos
Similar Questions
Knowledge Check
Let y=f(x)={e1x2ifx≠00ifx=0 then which of the following can best represent the graph of y=f(x)?
A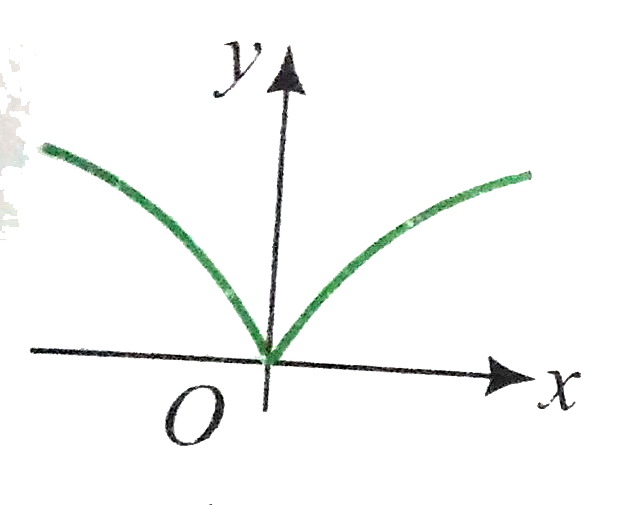 B
B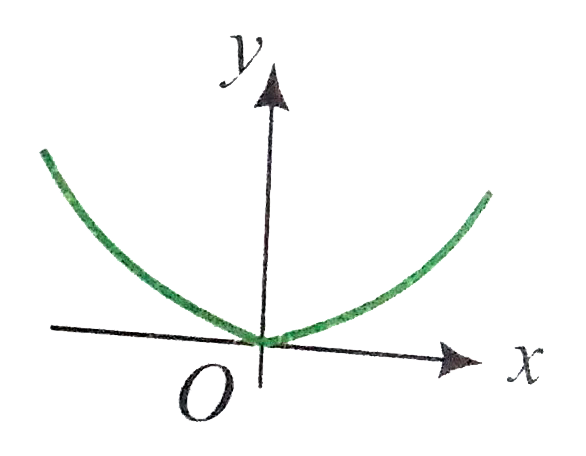 C
C D
D
If f(y)=y2−y−1,for0≤y<2=4y+1,for2≤y≤4, then
Af(y) is continuous aty=2Bf(y) is discontinuous aty=2Climy→2−f(y)=9Dlimy→2+f(y)=1Let f be a differential function satisfying the condition. f(xy)=f(x)f(y)for all x,y(≠0)∈Randf(y)≠0 If f'(1)=2, then f'(x) is equal to
A2f(x)Bf(x)2C2x f(x)D2f(x)x
If y=f(x) satisfies f(x+y)=2f(x)+xf(y)+y(f(x))1/3 for all x,y∈R,f'(0)=0 then (f(2))2 is equal to
View SolutionLetf(x+y)=f(x)f(y)for all x,y, wheref(0)≠0. If f'(0)=2, then f(x) is equal to
View SolutionLet f:R2→R be defined by f(x,y)=⎧⎨⎩x2yx4+y2,(x,y)≠(0,0)0 ,(x,y)=(0,0) Then, the directional derivative of f at (0,0) in the direction of the vector (1√2,1√2) is
View SolutionLet f(x,y)=⎧⎨⎩x2y2x2+y2(x.y)≠(0,0)0 (x,y)=(0,0) Then,
View SolutionLet f(x,y)={xyx2+y2,(x,y)≠(0,0)0 ,(x,y)=(0,0)
View Solution

