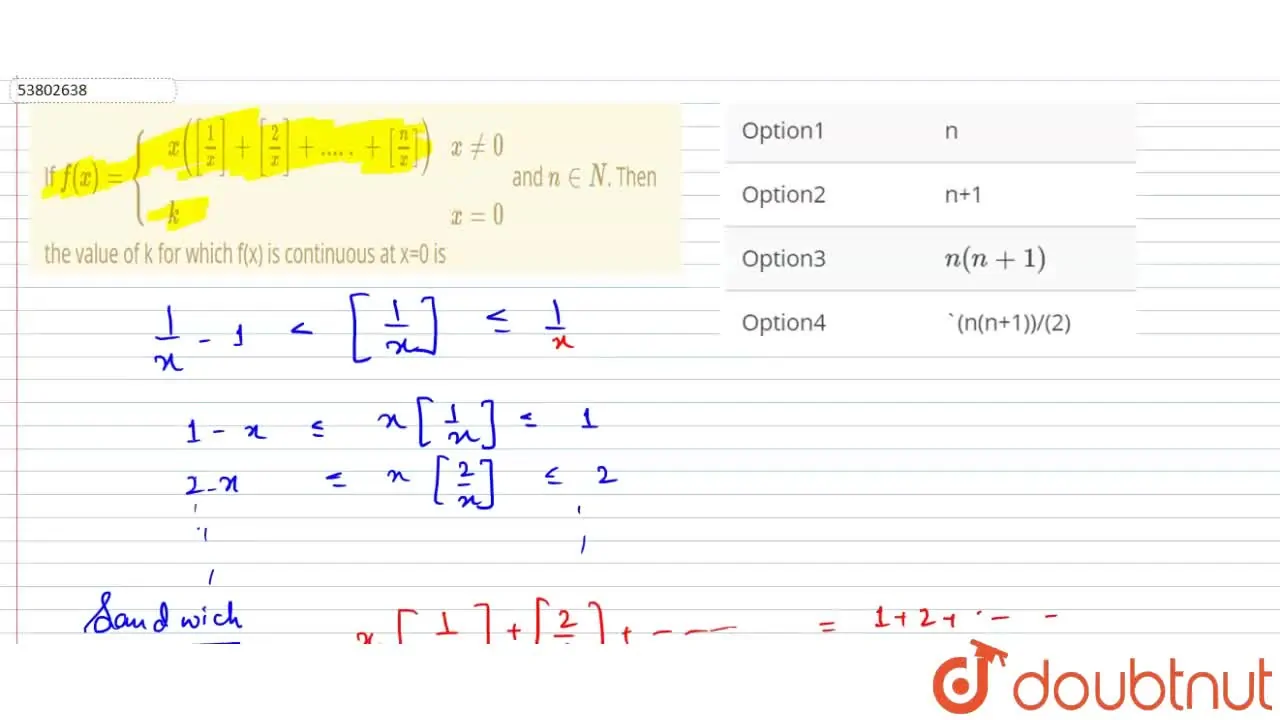
If f(x)={x([1x]+[2x]+.....+[nx])x≠0kx=0 and n∈N. Then the value of k for which f(x) is continuous at x=0 is
n
n+1
n(n+1)
(n(n+1))/(2)
The correct Answer is:D
For any x>0, we know that
1x−1<[1x]≤1x⇒1−x<x[1x]≤1
2x−1<[2x]≤2x⇒2−x≤x[2x]≤2
nx−1<[nx]≤nx⇒n−x<x[nx]≤n
∴n(n+1)2−nx<x([1x]+[2x]+....+[nx])≤n(n+1)2
But
limx→0{n(n+1)2−nx}=n(n+1)2and,limx→n(n+1)2=n(n+1)2
Therefore, by Sandwhich theoram, we obtain
limx→0x([1x]+[2x]+.....+[nx])=n(n+1)2
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
If f(x) = =⎧⎨⎩[tan(π4+x)]1/xx≠0kx=0
For what value of k f(x) is continuous at x=0 ?View SolutionLet f(x)=⎧⎪⎨⎪⎩∑x2[1|x|]r=0rx≠0kx=0 where [.] denotes the greatest integer function. The value of k for which is continuous at x=0, is
View Solutionf(x)=⎧⎨⎩(tan(π4+x))1/x,x≠0k,x=0 for what value of k, f(x) is continuous at x = 0 ?
View SolutionIf f(x)={xsin1xx≠0kx=0 is continuous at x=0, then the value of k is
View SolutionA function f(x) is defined as f(x)=[xmsin1x,x≠0,m∈Nand0,ifx=0 . The least value of m for which f'(x) is continuous at x=0 is
View SolutionIf f(x)=⎧⎨⎩√x+1−1√xfor x≠0kforx=0 and f(x) is continuous at x=0, then the value of k is
View SolutionIf f(x) = {1−cosxxx≠0xx=0 is continuous at x =0 then the value of k is
View SolutionIf the function f(X)={(cosx)1/xx≠0kx=0 is continuous at x=0, then the value of k, is
View SolutionIf f(x) = ⎧⎨⎩sin5xx2+2xx≠0k+12x=0 is continuous at x =0 then the value of k is
View SolutionIf f(x)={1−cosxxx≠0kx=0 is continuous at x=0, then the value of k is
View Solution