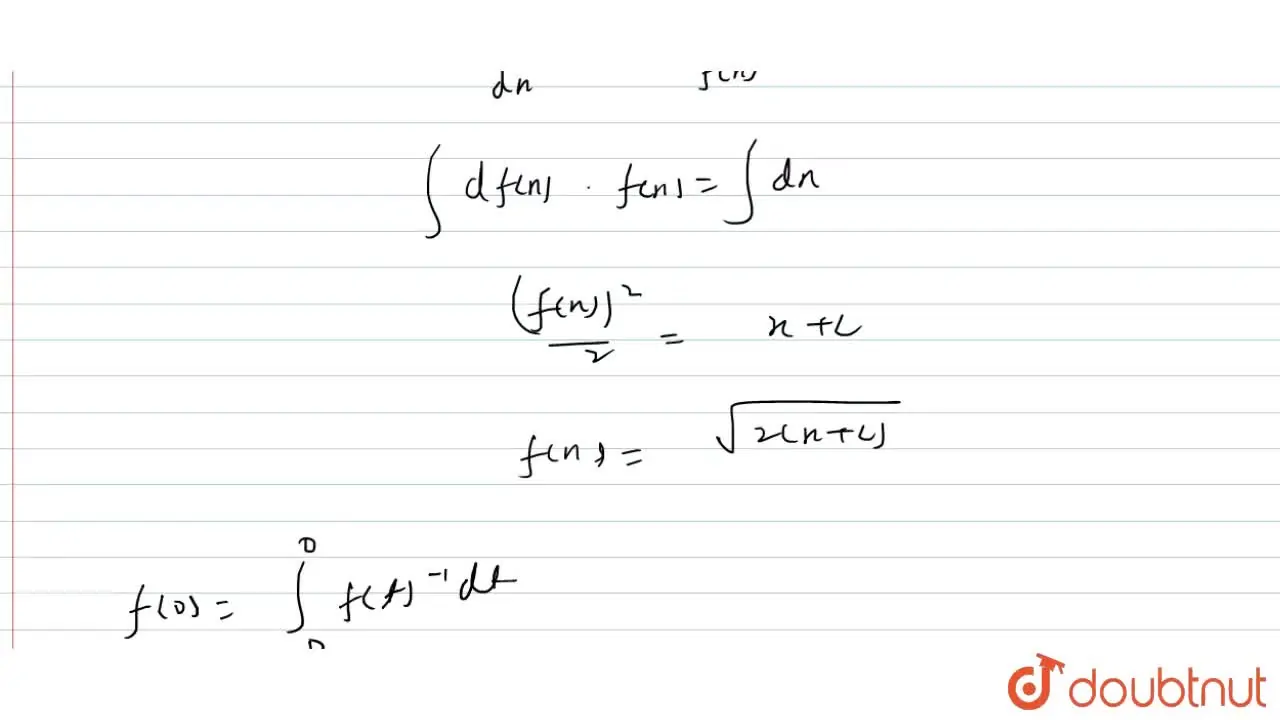If f(x)=∫x0{f(t)}−1dt, and ∫10{f(t}−1dt=√2, then f(x)=
A
√2x
B
√2logex
C
√3x−1
D
none of these
Video Solution
Text Solution
The correct Answer is:A
We have,
f(f)=x∫0{f(t)}−1dt
⇒f'(x)={f(t)}−1
⇒f'(x)f(x)=1
⇒2f(x)f'(x)=2⇒{f(x)}2=2x+C⇒f(x)=√2x+Cb
Now,
f(1)=√2⇒√2=√2+C⇒C=0
∴F(x)=√x
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type12videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise147videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
If f(x)=∫x0{f(t)}−1dtand∫10{f(t)}−1=√2, then
View SolutionIf f(x)=∫x1lnt1+tdt, then
View SolutionLet f(x)=∫x0f (t) dt equals
View SolutionIf f(x)=∫x2dt1+t4, then
View SolutionI ff(x)=∫x0dt(f(t))2and∫20dt(f(t))2=(6)13 then
View SolutionLet f1(x)=∫x0f(t)dt,f2(x)=∫x0f1(t)dtandf3(x)=∫x0f2(t)dt if f3(x)=A∫x0f(t)(x−t)2dt then the value of A is
View SolutionIf f(x)=∫sinx0cos−1tdt+∫cosx0sin−1tdt,0<x<π2 then f(π/4) is equal to
View SolutionIf ∫x0f(t)dt=ex−ae2x∫10f(t)e−tdt, then
View SolutionIf f(−x)+f(x)=0 then ∫xaf(t)dt is
View SolutionThe value of
sin2x∫0sin−1√tdt+cos2x∫0cos−1√tdt, isView Solution