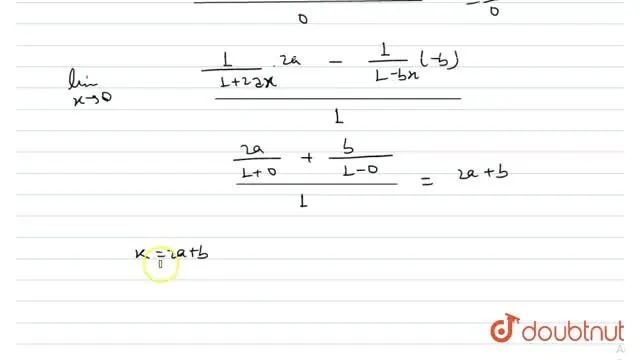
If f(x)={log(1+2ax)−log(1−bx)x,x≠0k,x=0 is continuous at x = 0, then value of k is
b + a
b - 2a
2a - b
2a + b
The correct Answer is:D
Given, f(x)={log(1+2ax)−log(1−bx)x,x≠0k,x=0
is continuous at x = 0.
∴f(0)=limx→0log(1+2ax)−log(1−bx)x [00form]
⇒k=limx→012ax+1(2a)−11−bx(−b)+1
⇒k=2a0+1+b1−0=2a+b [by L' Hospital's rule]
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CONTINUITYEXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS)60videos
CONTINUITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CIRCLE AND CONICSEXERCISE - All Questions74videos
CIRCLE AND CONICS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - DEFINITE INTEGRALSEXERCISE - MHT CET Corner22videos
DEFINITE INTEGRALS
Similar Questions
If f(x)={log(1+2ax)−log(1−bx)x,x≠0 k,x=0 is continuous at x = 0, then k is equal to
View SolutionIf f(x)={1−cosxx,x≠0k,x=0 is continuous at x = 0, then the value of k is
View Solutionf(x)={log(1+2ax)−log(1−bx)x,x≠0x=0
View SolutionIf f(x) =log(1−2x)−log(1−3x)x, x≠0=a, x=0 is continuous at x = 0 , then : a =
View SolutionIf f(x)=log1−3x(1+3x),x≠0=k,x=0
is continuous at x = 0, then the value of k isView SolutionIf f(x)=⎧⎨⎩sin5xx2+2x,x≠0k+12,x=0 is continuous at x = 0, then the value of k is
View SolutionIf f(x)={1−cosxxx≠0kx=0 is continuous at x=0, then the value of k is
View SolutionIf f(x)={xsin1xx≠0kx=0 is continuous at x=0, then the value of k is
View SolutionIf f(x)={x sin1x,x≠0k,x=0 is continuous at x=0, then the value of k is
View SolutionIf f(x) =log(1+3x)−log(1−2x)x, if x≠0=a, if x=0 is continuous at x = 0 , then a =
View Solution