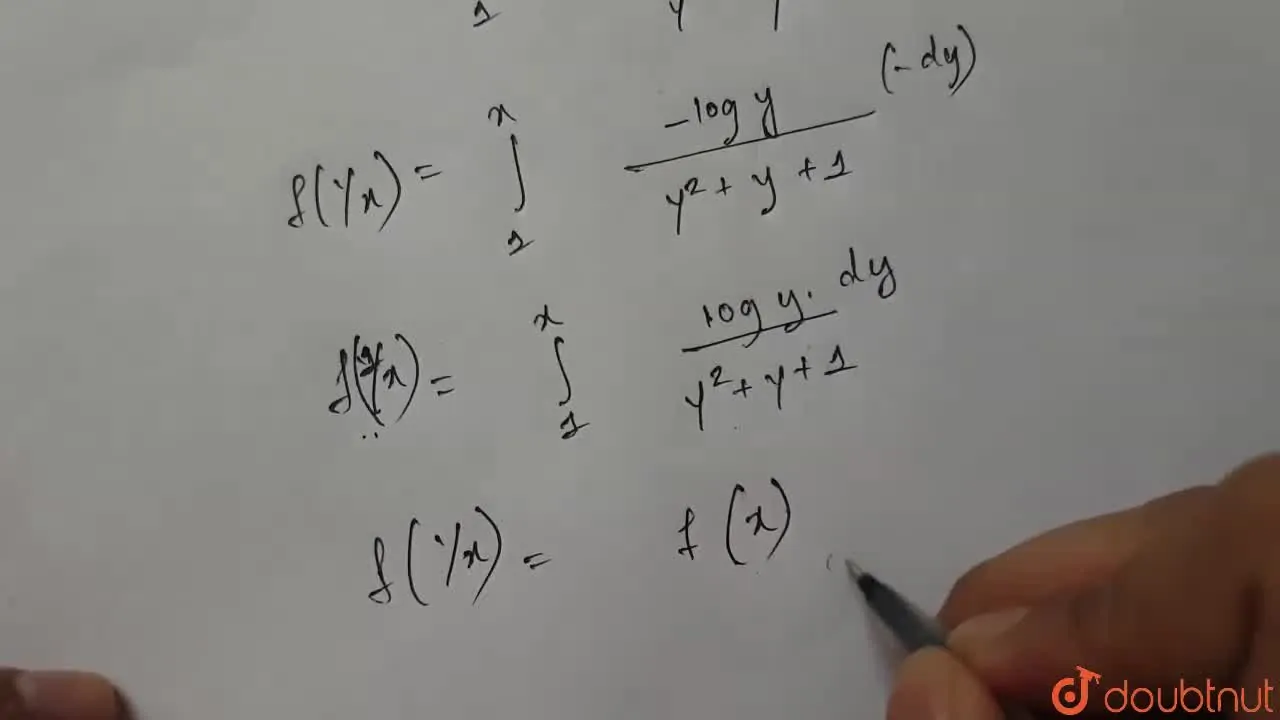If f(x)=∫x1(logt)(1+t+t2)dt∀x≥1, then prove that f(x)=f(1x).
The correct Answer is:NA
Given f(x)=∫1(x)logt1+t+t2dt
or f(1x)=∫1/x1logt1+t+t(2)dt
Let y=1t or dy=dtt2
∴f(1x)=∫x1log1y1+1y+1y2(−1y2dy)
=∫x1logy1+y+y2dy=f(x)
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - SCQ_TYPE113videos
DEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - MCQ_TYPE27videos
DEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - DEFINITE INTEGRATION EXERCISE - SOLVED EXAMPLE_TYPE20videos
DEFINITE INTEGRATION
- BOOK - CENGAGE ENGLISHCHAPTER - CURVE TRACINGEXERCISE - EXERCISES24videos
CURVE TRACING
- BOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer5videos
DETERMINANT
Similar Questions
Iff(x)=∫x1logt1+t+t2dx∀x≤1,thenprovethatf(x)=f(1x).
View SolutionIf f(x)=∫x2dt1+t4, then
View SolutionIf f(x)=∫x1logt1+t+t2, ∀x≥1, then f(2) is equal to
View SolutionStatement-1: If f(x)=∫x1loget1+t+t2dt, then
f(x)=f(1x)for all xgr0.
Statement-2:If f(x)=∫x1loget1+tdt, then f(x)+f(1x)=(logex)22View SolutionLet f(x)=∫x13t1+t2dt, where x>0, Then
View SolutionIf f(x)=∫x2xdt(logt)2,x≠0 then f(x) is
View SolutionIf f(x)=∫x2+1x2e−t2dt , then f(x) increases in
View SolutionIf f(x)=x2∫10f(t)dt+2, then
View SolutionGiven a function 'g' continous everywhere such that ∫10g(t)dt=2andg(1)=5. If f(x)=12∫x0(x−t)2g(t)dt, then the vlaue of f''(1)−f'(1) is:
View SolutionGiven a function 'g' continous everywhere such that ∫10g(t)dt=2andg(1)=5. If f(x)=12∫x0(x−t)2g(t)dt, then the vlaue of f'''(1)−f''(1) is:
View Solution