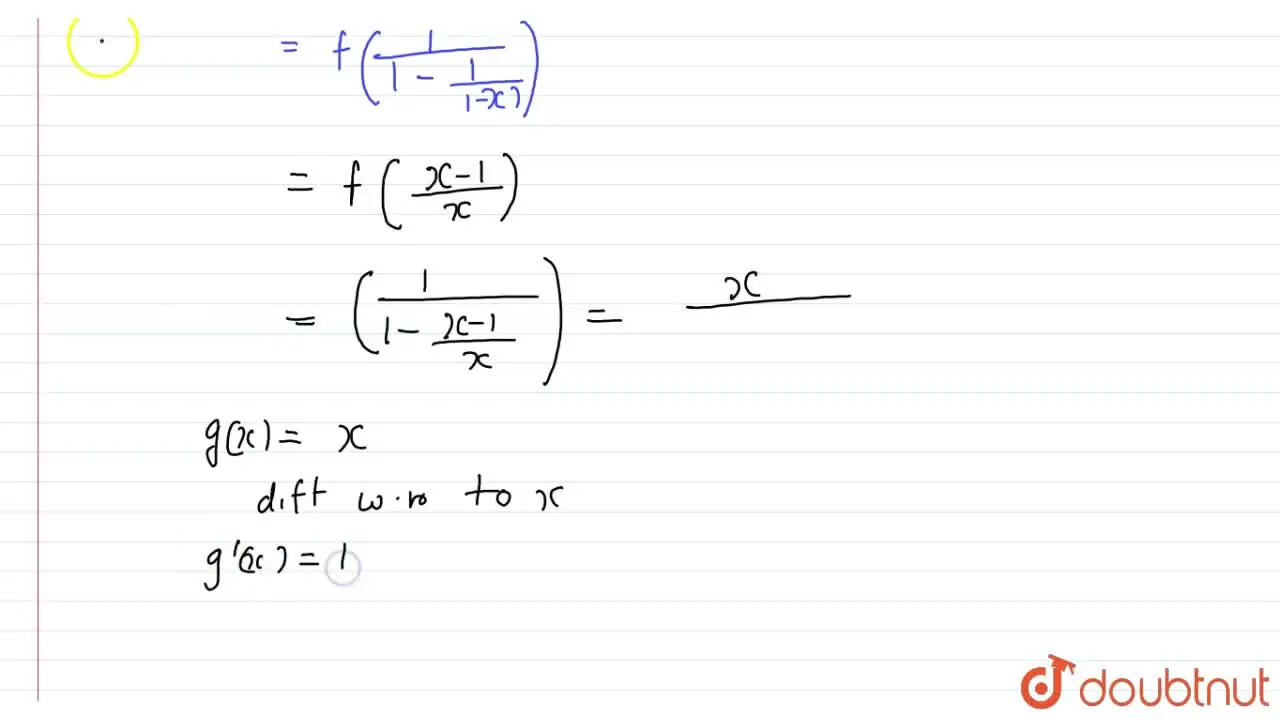If f(x)=11−x, then the derivative of the composite function f[f{f(x)}] is equal to
0
1/2
1
2
The correct Answer is:C
Clearly, f(x) is not defined at x=1.
Forr x∈R−{1}, we have
g(x)=f[f{f(x)}]=f[f(11−x)]=f⎛⎝11−11−x⎞⎠
⇒ g(x)=f(x−1x)=11−x−1x=x
∴ g'(x)=1 for all x∈R−{1}
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Exercise58videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test30videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test30videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Exercise17videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ELLIPSEEXERCISE - Chapter Test29videos
ELLIPSE
Similar Questions
Given the function f(x)=11−x , The points of discontinuity of the composite function f[f{f(x)}] are given by
View SolutionFind an anti-derivative of the function f(x)=1x
View SolutionIf the function f(x)=1x+2, then find the points of discountinuity of the composite function y=f{f(x)}.
View SolutionGiven f(x)=1x−1. Find the points of discontinuity of the composite function f(f(x)).
View SolutionGiven f(x)=1x−1 . Find the points of discontinuity of the composite function f(f(x)) .
View SolutionIf f(x)=x−1x+1 then f(2x) is equal to
View SolutionIf f(x)=x−1x+1 then f(2x) is equal to
View SolutionFind the derivative for function f(x)=x+1x with respect to x
View SolutionFind the derivative for function f(x)=x(x−1) with respect to x
View SolutionIf f(x)=x−1x+1, then f(2) is equal to
View Solution