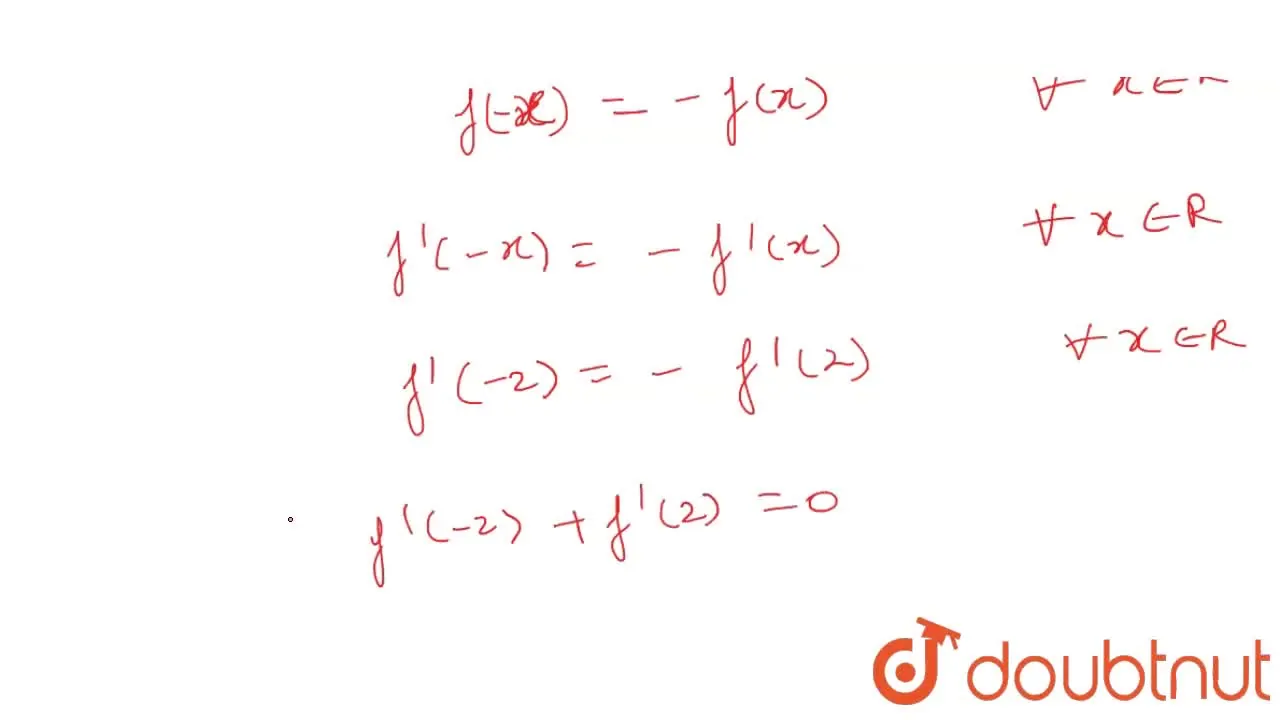If f(x−y),f(x)f(y)andf(x+y) are in A.P. for all x,y∈R and f(0)=0. Then,
f'(2)=f'(2)
f'(−3)=−f'(3)
f'(−2)+f'(2)=0
none of these
The correct Answer is:A
It is given that for all x,y∈R
f(x−y),f(x)f(y)andf(x+y)are in A.P
∴2f(x)f(y)=f(x−y)+f(x+y)for all x,y∈R
⇒2f(0)f(x)=f(−x)+f(x)for all x∈R[Replacing x by 0 and y by x]
⇒f(−x)+f(x)=for all x∈R
⇒f(−x)=−f(x)=for all x∈R
⇒−f'(−x)=−f'(x)=for all x∈R
⇒f'(−x)=f'(x)=for all x∈R
⇒f'(−2)=f'(2)=for all x∈R
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
If f(x−y),f(x)f(y),andf(x+y) are in A.P. for all x, y, and f(0)≠0, then
View SolutionLet f be a real function such that f(x−y),f(x)f(y) and f(x+y) are in A.P. for all x,y, ∈R. If f(0)≠0, then
View SolutionIf f(x−y),f(x)⋅f(y),f(x+y) are in for all x,y∈R and f(0)≠0, then
View SolutionLe f:R→Randg:R→R be functions satisfying f(x+y)=f(x)+f(y)+f(x)f(y)andf(x)=xg(x) for all x,y∈R.Iflimx→0g(x)=1 , then which of the following statements is/are TRUE ?
View SolutionLet f(x+y) + f(x-y) = 2f(x)f(y) for x, y∈R and f(0)≠0. Then f(x) must be
View SolutionLet f:R→R be a function given by
f(x+y)=f(x)f(y) for all x,y∈R
If f(x)≠0 for all x∈R and f'(0) exists, then f'(x) equalsView Solution|f(x)−f(y)|≤(x−y)2∀x,y∈Randf(0)=1 then
View SolutionLet f:R∈R be a function given by f(x+y)=f(x)f(y)for allx,y∈R
If (x)≠0,for all x∈Randf'(0)=log2,then f(x)=View SolutionLet f(x) be a differentiable function satisfying the condition f(xy)=f(x)f(y), where y≠0,f(y)≠0 for all x,y y∈R and f'(1)=2
The value of 1∫−1f(x)dx isView SolutionLet f be a continuous function satisfying f(x) f(y)=f(x)+f(y)+f(xy)-2 for all x,y ∈ R and f(2)=5 then limx→4f(x) is
View Solution